MAT9ORT

Bulk Data Entry

MAT9ORT – Material Property Definition, Form 9-Orthotropic

Description

Defines the material properties for linear, temperature-independent, and orthotropic materials for solid elements in terms of engineering constants.

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MAT9ORT	MID	E1	E2	E3	NU12	NU23	NU31	RHO
	G12	G23	G31	A1	A2	A3	TREF	GE

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MAT9ORT	21	1e6	1e3	1e3	0.1	0.1		1e5
	1e3	1e3		1e-6	1e-6	1e-6

Field	Contents
MID	Material identification number. Must be unique with respect to other MAT1, MAT2, MAT8, MAT9, and MAT9ORT definitions. No default (Integer > 0)
E1	Elastic modulus in 1-direction. No default (Real)
E2	Elastic modulus in 2-direction. No default (Real)
E3	Elastic modulus in 3-direction. No default (Real)
NU12	Poisson’s ratio for uniaxial loading in 1-direction. See comment 3. No default (Real)
NU23	Poisson’s ratio for uniaxial loading in 2-direction. See comment 3. No default (Real)
NU31	Poisson’s ratio for uniaxial loading in 3-direction. See comment 3. Default = NU23 (Real)
RHO	Mass density. No default (Real)
G12	Shear modulus on plane 1-2.
G23	Shear modulus on plane 2-3.
G31	Shear modulus on plane 3-1.
Ai	Coefficient of thermal expansion in the i-direction Default =0.0 (Real)
TREF	Reference temperature for the calculation of thermal loads. Default = blank (Real or blank)
GE	Structural element damping coefficient. See comment 5. Default = 0.0 (Real)

Comments

1.	This input definition is internally converted to an equivalent MAT9 definition on reading (Comment 6). This is reflected in echoed (ECHO) input data and all messaging.

2.	The material identification number must be unique for all MAT1, MAT2, MAT8, MAT9 and MAT9ORT entries.

3.	In general, is not the same as , but they are related by .

Furthermore, material stability requires that:

and

4.	It may be difficult to find all nine orthotropic constants. In some practical problems, the material properties may be reduced to normal anisotropy in which the material is isotropic in a plane (for example, plane 1-2), and has different properties in the direction normal to this plane.

In the plane of isotropy, the properties are reduced to:

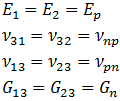
mat0ort_eq

with and

There are five independent material constants for normal anisotropy (Ep, En, vp, vnp, and Gn).

In case the material has a planar anisotropy, in which the material is orthotropic only in a plane, the elastic constants are reduced to seven (E1, E2, E3, v12, G12, G23, and G31).

5.	To obtain the damping coefficient GE, multiply the critical damping ratio, C/C0 by 2.0.

6.	Internal conversion from MAT9ORT to MAT9. The material property fields of the MAT9 entry are calculated internally from the MAT9ORT entry using the following formula:

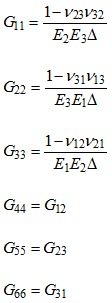
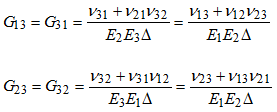
Where,

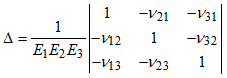
The values of , E and G for the expressions in the above equations in comment 7 are taken from the NUij , Ei and Gij fields respectively of this MAT9ORT entry where i, j € {1,2,3} and the values of G11, G22, G33, G44, G55, G66, G12, G13, and G23 (see above equations) are used to populate the G11, G22, G33, G44, G55, G66, G12, G13, and G23 fields (G12=G21, G13=G31 and G23=G32 due to symmetry) of the MAT9 entry. The remaining elements of the MAT9 entry (that is G14, G15, G24, and so on) are equal to zero.