MATHE

Bulk Data Entry

MATHE – Nonlinear Hyperelastic Material Property Definition

Description

The MATHE bulk data entry defines material properties for nonlinear hyperelastic materials. The Polynomial form is available and various material types (comment 3) can be defined by specifying the corresponding coefficients.

Format A

Generalized Mooney-Rivlin Polynomial (MOONEY), Reduced Polynomial (RPOLY), Physical Mooney-Rivlin (MOOR), Neo-Hookean (NEOH), and Yeoh Model (YEOH):

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MATHE	MID	Model		NU	RHO	TEXP	TREF
	C10	C01	D1	TAB1	TAB2		TAB4	TABD
	C20	C11	C02	D2	NA	ND
	C30	C21	C12	C03	D3
	C40	C31	C22	C13	C04	D4
	C50	C41	C32	C23	C14	C05	D5

Format B

Arruda-Boyce Model (Model=ABOYCE):

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MATHE	MID	Model		NU	RHO	TEXP	TREF
	C1			TAB1	TAB2		TAB4

Format C

Ogden Material Model (Model=OGDEN):

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MATHE	MID	Model	NA	NU	RHO	TEXP	TREF
	MU1	ALPHA1	D1	TAB1	TAB2		TAB4
	MU2	ALPHA2		MU3	ALPHA3
	MU4	ALPHA4		MU5	ALPHA5

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MATHE	2	MOONEY
	80	20	0.001

Field	Contents
MID	Unique material identification number. No default (Integer > 0)
Model	Specifies the type of hyperelastic material model MOONEY – Selects the generalized Mooney-Rivlin hyperelastic model MOOR – Physical Mooney-Rivlin model RPOLY – Reduced Polynomial model NEOH – Neo-Hookean model YEOH – Yeoh model ABOYCE - Selects the Arruda-Boyce material model OGDEN - Ogden material model Default = MOONEY (Character, <MOONEY, MOOR, RPOLY, NEOH, YEOH, ABOYCE, OGDEN, or blank>)
NU	Poisson's ratio No default (Real)
RHO	Material density No default (Real)
TEXP	Coefficient of thermal expansion No default (Real)
TREF	Reference temperature No default (Real)
NA	Order of the distortional strain energy polynomial function if the type of the model is generalized polynomial (MOONEY) or Reduced Polynomial (RPOLY). It is also the Order of the Deviatoric Part of the Strain Energy Function of the OGDEN material (Format C). Default = 2 (0 < Integer < 5)
ND	Order of the volumetric strain energy polynomial function (see comment 2). Default = 1 (Integer > 0)
Cpq	Material constants related to distortional deformation. No default (Real)
Dp	Material constants related to volumetric deformation. No default (Real > 0.0)
TAB1	Table identification number of a TABLES1 entry that contains simple tension-compression data to be used in the estimation of the material constants, Cpq, related to distortional deformation. The x-values in the TABLES1 entry should be the stretch ratios and y-values should be values of the engineering stress. (Integer > 0 or blank)
TAB2	Table identification number of a TABLES1 entry that contains equi-biaxial tension data to be used in the estimation of the material constants, Cpq, related to distortional deformation. The x-values in the TABLES1 entry should be the stretch ratios and y-values should be values of the engineering stress. (Integer > 0 or blank)
TAB4	Table identification number of a TABLES1 entry that contains pure shear data to be used in the estimation of the material constants, Cpq, related to distortional deformation. The x-values in the TABLES1 entry should be the stretch ratios and y-values should be values of the nominal stress. (Integer > 0 or blank)
TABD	Table identification number of a TABLES1 entry that contains Volumetric part (Dp) of the data to be used in the estimation of the material constants. The x-values in the TABLES1 entry should be the pressure and y-values should be values of the volumetric change. TABD can only be used to fit Volumetric data for Format A, additionally, only first-order fitting is currently supported (only D1 value is sourced from the TABD data). (Integer > 0 or blank)
C1	Locking stretch (Model = ABOYCE). See comment 5. Default = 0.0 (Real)
m	Defines the value of β (Model = ABOYCE). See comment 5. No default (Real)
MUi, ALPHAi	Material Constants for the Ogden Material Model (Model = OGDEN). See comment 6.

Comments

1.	If the Cpq and TAB# fields are input, the Cpa (≠ 0.0) values are overwritten with the curve fit values based on the corresponding TAB# tables. However, any Cpq values set to 0.0 are not overwritten.

2.	The Generalized polynomial form (MOONEY) of the Hyperelastic material model is written as a combination of the deviatoric and volumetric strain energy of the material. The potential (U) is written in polynomial form, as follows:

Generalized polynomial form (MOONEY):

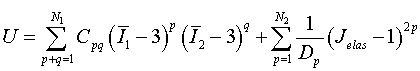
polynomial_form

Where,

N1 is the order of the distortional strain energy polynomial function (NA)

N2 is the order of the volumetric strain energy polynomial function (ND). Currently only first order volumetric strain energy functions are supported (ND=1).

Cpq are the material constants related to distortional deformation (Cpq)

, are invariants internally calculated by OptiStruct

Dp are material constants related to volumetric deformation (Dp). These values define the compressibility of the material.

Jelas is the elastic volume strain calculated internally by OptiStruct

3.	The polynomial form can be used to model the following material types by specifying the corresponding coefficients (Cpq, Dp) on the MATHE entry:

Physical Mooney-Rivlin Material (MOOR):

N1 = N2 =1

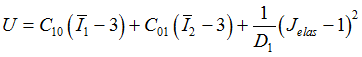
Reduced Polynomial (RPOLY):

q=0

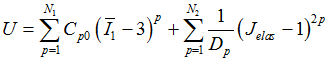
•	Neo-Hooken Material (NEOH)

N1= N2 =1, q=0

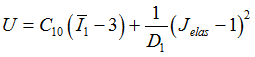
•	Yeoh Material (YEOH)

N1 = N2 =3, q=0

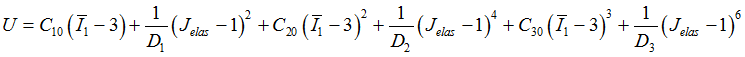
Some other material models from the Generalized Mooney Rivlin model are as follows:

Three term Mooney-Rivlin Material:

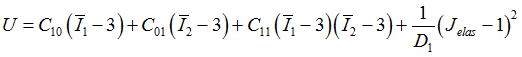
Signiorini Material:

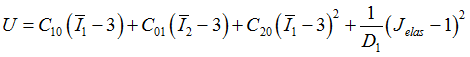
Third Order Invariant Material:

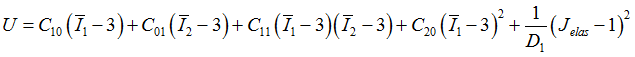
Third Order Deformation Material (James-Green-Simpson):

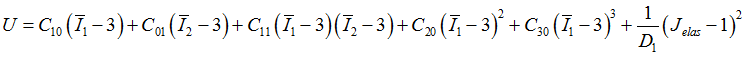
4.	The MATHE hyperelastic material supports CTETRA (4, 10), CPENTA (6, 15), and CHEXA (8, 20) element types.

5.	The Arruda-Boyce model (ABOYCE) is defined as follows:

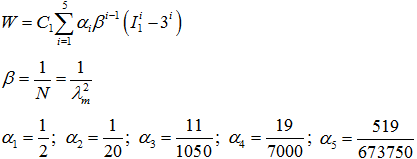
mathe_arruda_boyce

6.	The Ogden Material model (OGDEN) is defined as follows:

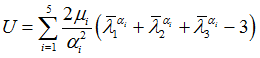
Where, are the three principal stretches, are defined by the MUi fields, and ai are defined by the ALPHAi fields, and Ni is the order of the Deviatoric part of the strain energy function defined on the NA field.

7.	This card is represented as a material in HyperMesh.