|
»Click here to display Table of Contents«
|
MBPTDCV |
|
|
|
|
|
MBPTDCV |
|
|
|
|
|
»Click here to display Table of Contents«
|
MBPTDCV |
|
|
|
|
|
MBPTDCV |
|
|
|
|
MBPTDCV – Multi-body Point to Deformable Curve Constraint
Defines a Point to Deformable Curve Constraint.
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
(10) |
MBPTDCV |
JID |
GID |
DCID |
|
|
|
|
|
|
|
Field |
Contents |
JID |
Joint identification number. No default (Integer > 0) |
GID |
Grid identification number corresponding to the point which is sliding on the deformable curve. No default (Integer > 0) |
DCID |
Deformable curve (MBDCRV) identification number. No default (Integer > 0) |
Comments
| 1. | The deformable curve is generated using the CUBIC spline interpolation which requires assumptions on the second derivative of the interpolating function at either end of the curve. The keywords NATURAL, PARABOLIC, PERIODIC and CANTILEVER represent the four standard assumptions defined as follows: |
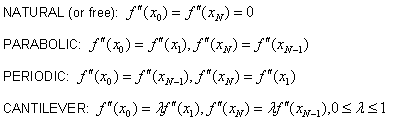
Note that λ =0.0 implies NATURAL (or free) end conditions and λ =1.0 implies PARABOLIC end conditions.
| 2. | The MBPTDCV element is not supported by the Force Imbalance method of static equilibrium. |
| 3. | In most cases, the interpolation produces a smooth curve but in some cases, it produces a curve that wiggles too much. In those cases, the TENSION parameter may be specified to smooth out the wiggles in the curve. A TENSION value of unity is a good first guess. After that, higher values of TENSION may be tried, if necessary. |
| 4. | The deformable element itself does not possess any inherent inertia, stiffness or damping properties. You must include other modeling elements to capture those effects. |
See Also:
