|
»Click here to display Table of Contents«
|
Seam Weld Fatigue Analysis (New Feature) |
|
|
|
|
|
Seam Weld Fatigue Analysis (New Feature) |
|
|
|
|
The method implemented in OptiStruct is based on a research paper Fatigue Life Prediction of MAG-Welded Thin-Sheet Structures published by M. Fermér, M Andréasson, and B Frodin. The method is a hot spot stress approach applicable to thin metal sheets. Hot spot stress is calculated from grid point forces at weld line. The method showed a good agreement with laboratory test results for sheet thickness between 1.0 mm and 3.0 mm. The method typically requires two S-N curves. One is a bending S-N curve which is dominated by bending stress, and the other is a membrane S-N curve which dominated by membrane stress.
Seam Weld Fatigue Analysis implementation in OptiStruct consists of the following modeling requirements.
| 1. | Weld sections to be analyzed for seam weld fatigue should be meshed with CQUAD4 elements whenever possible. CTRIA3 elements may be used for corner weld if inevitable and for closing the end of weld line if necessary. Other element types are currently not supported for Seam Weld Fatigue. |
| 2. | The weld should be modeled by a single or double row of CQUAD4 elements. If a 2 sided fillet is to be modeled, a third row of CQUAD4 may be used. |
| 3. | The thickness of the weld element is the same as the effective throat. |
| 4. | The mesh size around the weld should be as regular as possible. Although this method is less sensitive to mesh size, a mesh size of about 10 mm would be a good choice according to Fermér, Andréasson, Frodin. This paper showed that large hot spot stress differences did not exist between mesh size 12 mm and mesh size 5 mm in case of a regular mesh. |
| 5. | The weld element should have a dedicated property ID that is referenced by the PIDi fields of the FATSEAM Bulk Data Entry. For more information, refer to Input below. The property should be stiff enough to be a force transducer. |
| 6. | The weld element normal direction should point outwards such that the normal direction is toward the weld toe, not toward the weld root. The normal direction of weld element plays a critical role in determining the weld toe and the surface to be examined on the base of the weld. |
A weld can be used to join two parts together. Welds vary in shapes and sizes depending on the type of joint that is required. For example, welds for Fillets and Overlap Joints are different. Typically, a weld consists of the following parts:
| • | Face |
| • | Toes |
| • | Throat |
| • | Root |
| • | Legs |
The face of a weld is the outer surface of the weld that is visible to you. The Toes are the points where the base material of the connected plates intersects with the weld material along the weld face. The weld throat is the distance between the root and the center of the face. The weld root is point of deepest weld penetration and it is opposite to the weld face. The weld legs extend from the root of the weld to the toes.
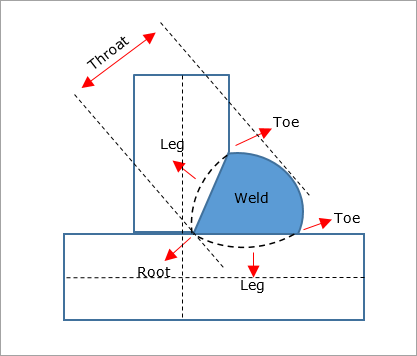
Figure 1(a): Basic Weld Structure
This section provides a basic overview of stress concentrations in welded structures and a few recommendations for good weld design. This section should not be considered as a complete weld design guide and does not cover an exhaustive list of weld design recommendations.
All welds contain stress concentrations which will reduce the fatigue life. A local stress concentration occurs at the toe of the weld and is controlled by the welding process conditions. This stress concentration is embedded in a macroscopic stress concentration that is a result of the design of the weld joint.
| a) | Weld shape based stress concentration: |
Figure 1(b) shows the stress concentration at the toe of a weld. Its magnitude depends on the flank angle, θ, local weld toe radius, r, and plate thickness, t. The concept of a weld reinforcement is a misnomer as you can see that the stress concentration actually increases with increasing weld metal, that is, an increase in flank angle, θ.
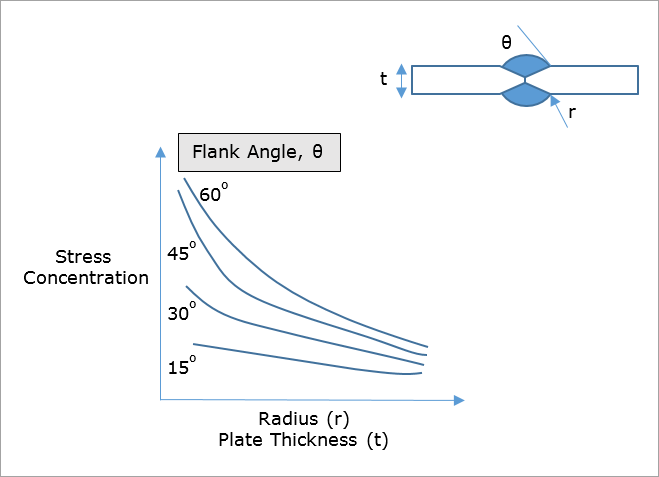
Figure 1(b): Stress concentration vs Weld Radius and Plate Thickness for Seam Weld Fatigue.
| b) | Weld design based stress concentration: |
The second stress concentration comes from the joint design. Stress concentrations arise whenever there is a change in stiffness in the structure. It can result from either an increase of decrease in stiffness. For example a hole in a plate will have about the same stress concentration as a rigid boss added to the plate. Here are some examples of weld joints contrasting good and poor design practice.
First you need to consider a cover plate welded to a bending beam. A large stress concentration exists at the end of the cover plate because of the large change in stiffness. A better design is shown on the right side where there is a more gradual change in stiffness.
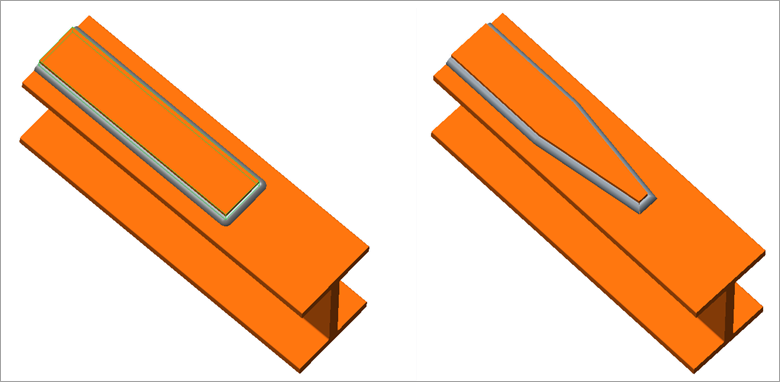
Figure 2: (a) Incorrect weld design (b) Correct weld design: Gradual stiffness gradient
A second source of stress concentration is unintentional bending stresses caused by asymmetric geometries. The design on the left will have larger bending stresses than the double lap joint on the right side.
Figure 3: (a) Incorrect weld design (b) Correct weld design: Double lap joint Symmetric geometry
Welding plates of differing thicknesses or widths is always problematic. Just as above, the easiest geometry to weld has the largest stress concentration. ou should always consider moving the welds to lower stress areas in the structure and have a gradual transition in stiffness such as the joint shown on the right side below.
Figure 4: (a) Incorrect weld design (b) Correct weld design: Gradual stiffness transition
OptiStruct supports certain types of welds for Seam Weld Fatigue analysis. The type can be selected using the WTYPE field on the FATSEAM Bulk Data Entry.
| • | Note that only one row of elements can be defined for the weld face elements or either of the weld legs. |
| • | The damage calculation locations are automatically chosen based on the weld type (as explained in the sections below). With the exception of the throat damage location, both the root and toe damage locations are evaluated based on the grid point forces and subsequent stresses induced in the corresponding elements adjacent to the weld elements. For throat damage, the weld element grid point forces, and subsequent stresses are directly considered. |
| • | OptiStruct currently supports the following weld types. |
A fillet weld is a weld joining two sheets at an angle. Typical failure locations are marked in the Figure 5(a). A fillet weld may be modeled by inclined CQUAD4 as in Figure 5(b). Depending on how much the weld penetrates, the weld may be modeled by a single or double row of CQUAD4. If a Two-sided fillet is to be modeled, three rows of CQUAD4 may be used.
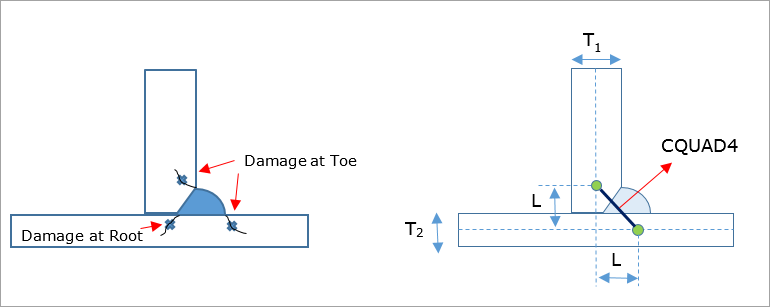
Figure 5: (a) Structure of a Fillet Weld. (b) T-Joint Seam weld element representation
OptiStruct evaluates failures at root and toe when a weld element is CQUAD4. If CTRIA3 is used for a weld element, only toe is evaluated.
One-sided One Row
For a One-sided One Row T-joint, the weld element normal direction should point towards the weld toe. The nodes of the weld element are in line with the weld toes. The length should be determined by the actual dimensions of the weld element (typically L=T1+T2).
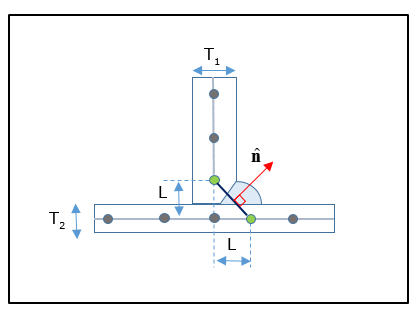
Figure 6: Representation of a One-sided T-Joint Fillet Weld with One row of CQUAD4 elements
The thickness of the weld element is the effective weld throat (typically it is equal to 1.414*L).
One-sided Two Row
Multiple rows are recommended for welds where the weld penetration is high and the weld typically forms the basis for contact between the two plates. Such welds are more rigid compared to welds where the penetration is lower, thereby additional rows of weld shell elements are required to capture the behavior. In Figure 7, you can clearly see that the weld has penetrated more than the weld in Figure 6. For a One-sided Two Row T-joint, the two weld element normal directions should point towards the weld toe. The length should be determined by the actual dimensions of the weld element (typically L=T1+T2).
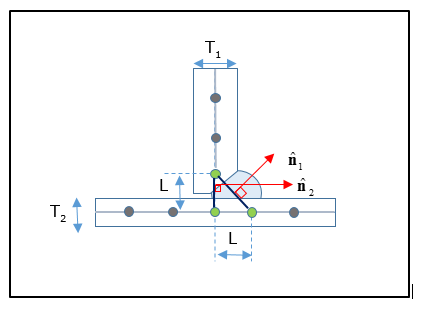
Figure 7: Representation of a One-sided T-Joint Fillet Weld with Two rows of CQUAD4 elements.
The thickness of the weld element is recommended to be set equal to 0.35*L.
Two-sided Two Row
For a Two-sided Two Row T-joint, the weld element normal directions should point towards the corresponding weld toe. The nodes of the weld elements are in line with the corresponding weld toes. The length should be determined by the actual dimensions of the weld element (typically L=T1+T2).
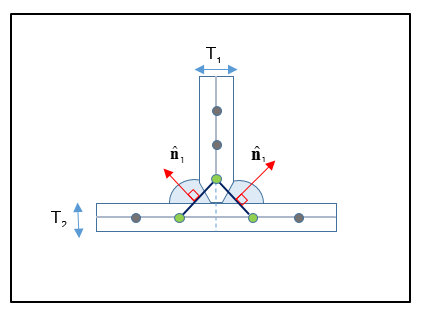
Figure 8: Representation of Two-sided T-Joint Fillet Weld with Two rows of CQUAD4 elements
The thickness of the weld element is the effective individual weld throat (typically it is equal to 1.414*L).
Two-sided Three Row
Multiple rows are recommended for welds where the weld penetration is high and the weld typically forms the basis for contact between the two plates. Such welds are more rigid compared to welds where the penetration is lower, thereby additional rows of weld shell elements are required to capture the behavior. In Figure 9, you can clearly see that the welds have penetrated more than the welds in Figure 8. For a Two-sided Three Row T-joint, the two weld element normal directions should point towards the corresponding weld toe. The weld element normal for the central vertical element can point to either weld toe.
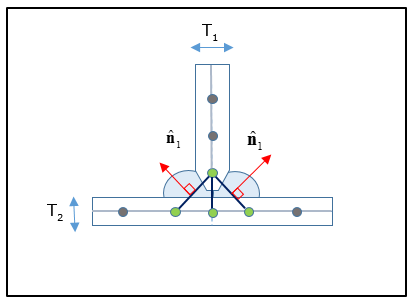
Figure 9: Representation of a Two-sided T-Joint Fillet Weld with Three rows of CQUAD4 elements
For a cross-joint, all weld elements associated with one cross joint weld should be specified in a single FATSEAM entry, otherwise OptiStruct will treat the cross-joint fillet weld as separate multiple welds and may output unexpected results. Additional requirement for a cross-joint is that the joint should be symmetric.
One-sided One Row
For a One-sided One Row Cross-joint, the weld element normal direction should point towards the corresponding weld toe.
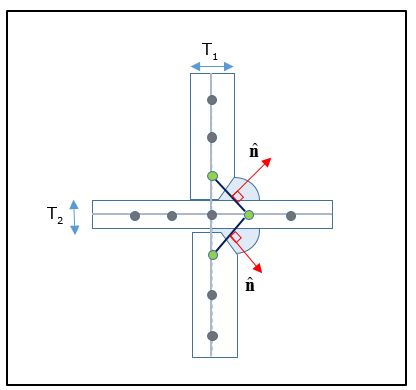
Figure 10: Representation of a One-sided Cross-Joint Fillet Weld with One row of CQUAD4 elements each
One-sided Two Row
Multiple rows are recommended for welds where the weld penetration is high and the weld typically forms the basis for contact between the two plates. Such welds are more rigid compared to welds where the penetration is lower, thereby additional rows of weld shell elements are required to capture the behavior. In Figure 11, you can clearly see that the welds have penetrated more than the welds in Figure 10. For a One-sided Two Row Cross-joint, the weld element normal direction should point towards the corresponding weld toe. The vertical weld element normals should also point towards the corresponding weld toe.
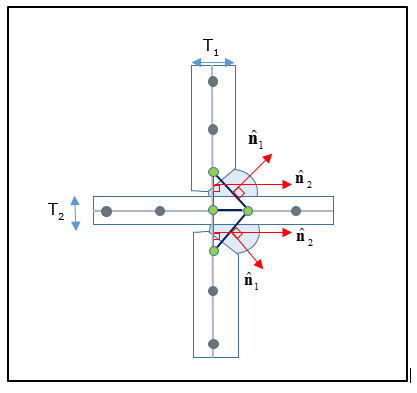
Figure 11: Representation of a One-sided Cross-Joint Fillet Weld with Two rows of CQUAD4 elements each
Two-sided Two Row
For a Two-sided Two Row Cross-Joint, the weld element normal direction should point towards the corresponding weld toe.
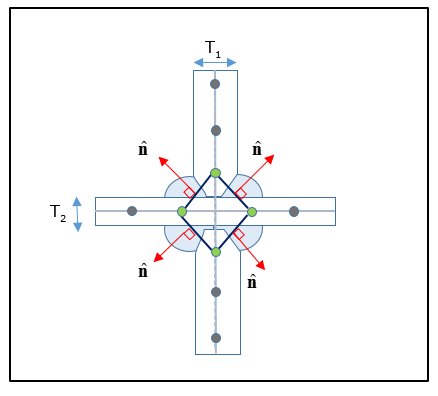
Figure 12: Representation of a Two-sided Cross-Joint Fillet Weld with Two rows of CQUAD4 elements each
Two-sided Three Row
Multiple rows are recommended for welds where the weld penetration is high and the weld typically forms the basis for contact between the two plates. Such welds are more rigid compared to welds where the penetration is lower, thereby additional rows of weld shell elements are required to capture the behavior. In Figure 13, you can clearly see that the welds have penetrated more than the welds in Figure 11.
For a Two-sided Three Row Cross-Joint, the weld element normal direction should point towards the corresponding weld toe. The normals of the vertical weld elements can point towards either weld toe on each side.
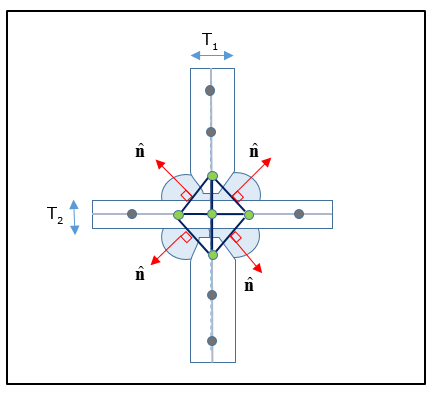
Figure 13: Representation of a Two-sided Cross-Joint Fillet Weld with Three rows of CQUAD4 elements each
An Overlap weld is a weld joining two overlapped sheets in parallel. Figure 14 shows possible failure locations. OptiStruct evaluates these locations. Typical failure locations are marked in the Figure 14. An Overlap weld may be modeled by inclined and vertical CQUAD4. Depending on how much the weld penetrates, the weld may be modeled by a single or double row of CQUAD4.
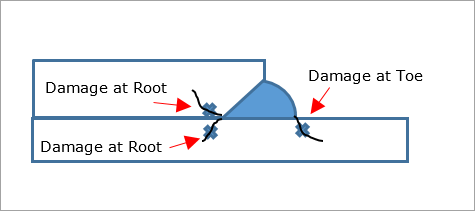
Figure 14: Structure of an Overlap Weld
Meshing rules are the same as that for fillet weld. Normal direction of weld element should be toward weld toe. Weld nodes should be along the line of the weld toe. Weld element thickness should be effective weld throat. In laser weld, failure at weld throat is evaluated as well as weld toe and weld root.
Multiple rows are recommended for welds where the weld penetration is high and the weld typically forms the basis for contact between the two plates. Such welds are more rigid compared to welds where the penetration is lower, thereby additional rows of weld shell elements are required to capture the behavior. The typical length of the weld element is L=T1+T2.
Typical weld element thickness is about 0.27*L.
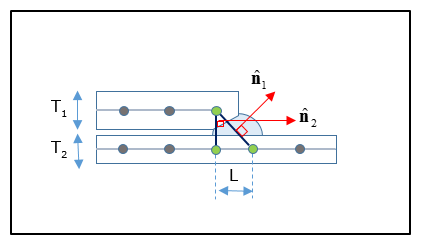
Figure 15: Representation of a two row Overlap weld
For overlap, weld element thickness should be 2 times the thickness of the thinner sheet. Its minimum thickness is 3mm. For laser edge overlap, weld element thickness should be effective weld throat. It is about 0.7* the upper sheet thickness.
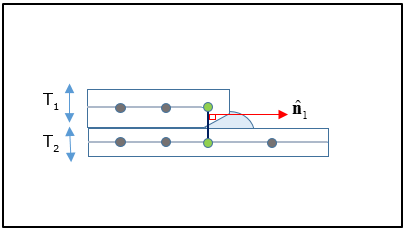
Figure 16: Representation of a one row Overlap weld or Laser Edge Overlap Weld
The previous weld can also be modeled as shown in Figure 17.
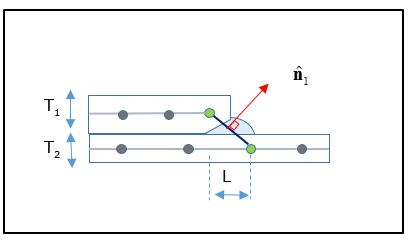
Figure 17: Representation of an alternative approach for a one row Overlap or Laser Edge Overlap
The thickness of the weld element should be the weld width. The weld width should be 90% of the thickness of the thinner sheet. Its minimum thickness is 1 mm. The Laser Overlap welds are intended for very thin sheets (> 1 mm).
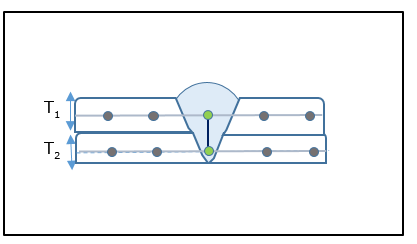
Figure 18: Representation of a Laser Overlap weld
Failure evaluation points differ from one weld type to another. The following sections provide information about which locations of the weld elements are used for failure evaluation in Seam Weld Fatigue Analysis. Figure 19(a) shows how the identification points are illustrated in subsequent images.
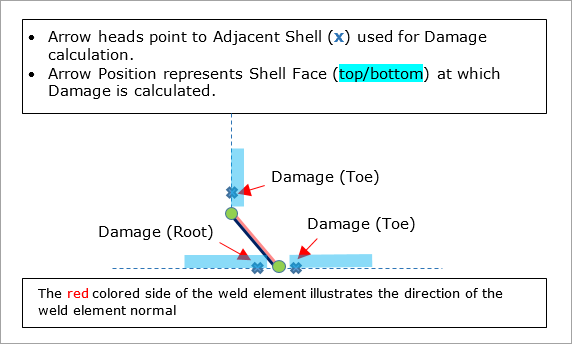
Figure 19(a): Illustrative image to show the attributes for proper identification of entities
The weld toe and root locations are evaluated. Throat location is not evaluated. Note that arrows in the Figures 19 and 20 indicate surfaces for evaluation (surface of the shell elements adjacent to the weld element).
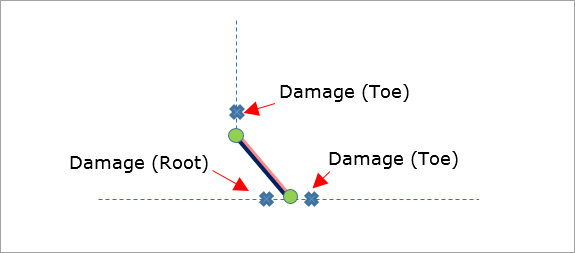
Figure 19(b): Failure Locations for One Row Fillet
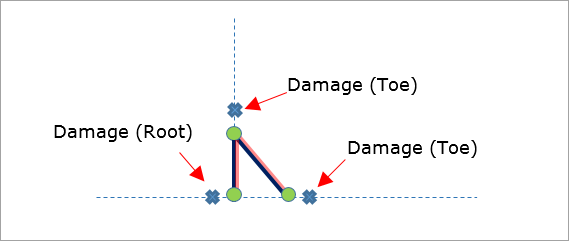
Figure 20: Failure Locations for Two Row Fillet
The weld toe and root elements are marked in Figures 21, 22, and 23. The weld throat is not evaluated.
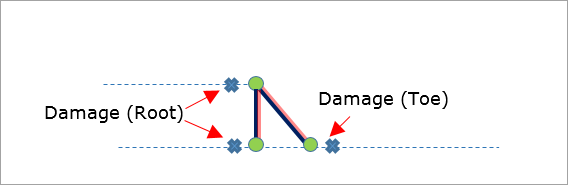
Figure 21: Failure Locations for Two Row Overlap
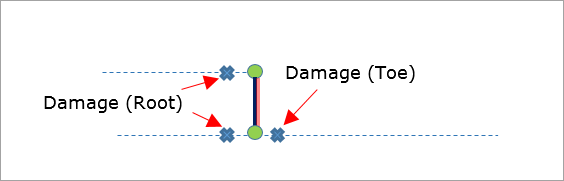
Figure 22: Failure Locations for One Row Overlap
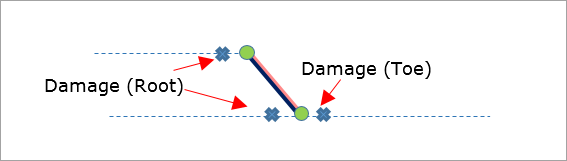
Figure 23: Failure Locations for One Row Overlap (Alternative)
The weld throat and root elements are marked in Figure 24. Both sides of the throat element are evaluated because either side of the throat can have a crack.
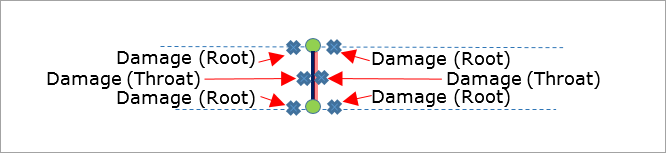
Figure 24: Failure Locations for Laser Overlap
Throat location has to be evaluated. Thus weld should be modeled with a single row in order to get a realistic result.
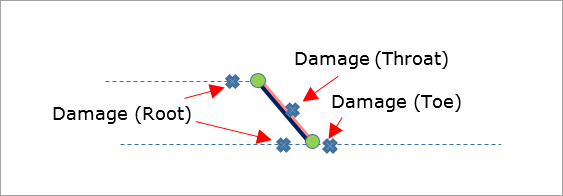
Figure 25: Failure Locations for Laser Edge Overlap
Note the surface where weld throat is evaluated. This surface is determined by normal direction of the weld element.
OptiStruct calculates hot spot stress based on grid point force of a toe/root element. In the original approach suggested by Fermér, Andréasson, Frodin, grid point forces contributed to the element of interest were directly used without any “adjustment”. Later research [P. Fransson and G. Pettersson, 2000] showed that averaging grid point forces made grid point forces less mesh sensitive. The calculation method implemented in OptiStruct includes weighted averaging of grid point forces, as outlined below.
| 1. | OptiStruct identifies potential damage locations at weld toe, weld root, weld throat and their evaluation surface from weld elements location and its normal direction (as shown in previous sections). |
| 2. | For the corresponding root and toe damage locations (in adjacent elements), and in the throat (in the weld element), local coordinate systems are constructed. The local X axis is constructed in the direction perpendicular to and away from the corresponding weld element face at the center of the adjacent element on the weld line (the X axis is in located in the plane of the adjacent element). The local Y axis is constructed perpendicular to this X axis in the plane of the adjacent element. |
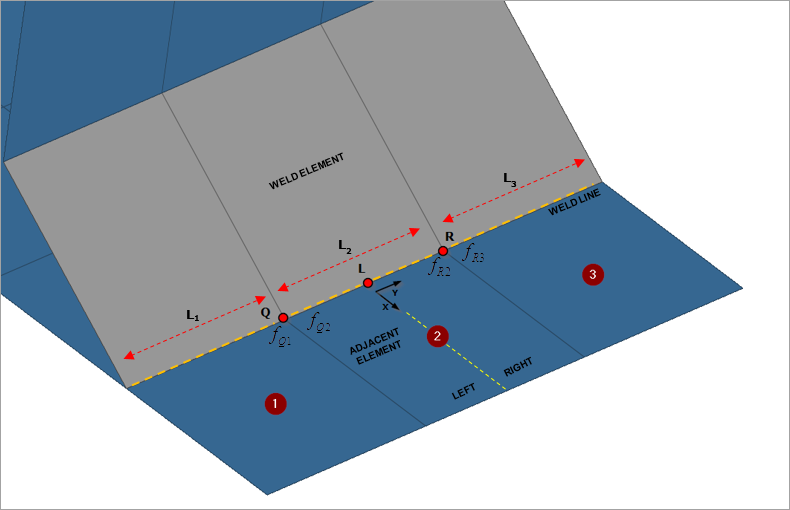
Figure 26: Example Illustration for Seam Weld Stress Calculation
| 3. | Grid point forces are calculated at grids (Q and R) of the adjacent element (2) along the weld line. Grid point force contributions are sourced from elements attached (1 and 3) to the adjacent element. |
Grid point forces are calculated as:
Moments are written as:
| 4. | At each node (Q and R) of the adjacent element that lies on the weld line, averaged grid point forces/moments weighted by length of the adjacent element and the attached element on the weld toe line are calculated. |
Weighted forces are written as:
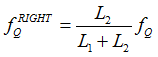
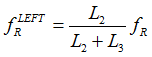
Weighted moments are written as:
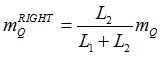
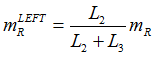
| 5. | Line Forces and Moments are calculated based on the weighted grid point forces and moments. These line forces and moments from both ends of the adjacent element on the weld line are averaged to generate the line force and moment at the midpoint (L). |
Line Forces are calculated as:
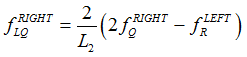
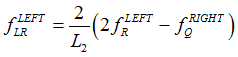
Line Moments are calculated as:
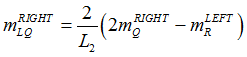
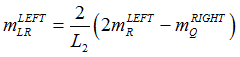
The averaged line forces and moments at the midpoint, L, for element 2 are:
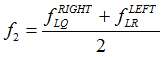
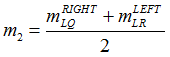
| 6. | The line force and moment at the midpoint are then resolved in the local coordinate system constructed in step 2 to generate  and  , respectively. This force and moment pair leads to tensile and bending stresses in the adjacent element with respect to the weld line. These are the forces that are used to calculate stresses. |
| 7. | Stresses are then calculated normal to the weld line for the adjacent element from this force moment pair. Stresses are calculated for both top and bottom of the shell element, and depending on the type of weld, either one or both are used for Fatigue calculations. This is the final hot spot stress used in further S-N Fatigue Damage Evaluation. For addition information, refer to S-N of Uniaxial Fatigue Analysis. |
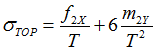
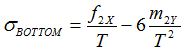
Fatigue Properties for Seam Weld Analysis
There are a few fatigue properties relevant to Seam Weld Fatigue Analysis that allow you to control the fatigue behavior.
Experiments show that two types of SN curves are required to perform Seam Weld Fatigue Analysis based on a method suggested by M. Fermér, M Andréasson, and B Frodin. Based on lab tests, two SN curves were plotted (Figure 27). The upper curve is obtained in tests where the maximum stress is dominated by Bending Moment (
) and the lower curve is obtained from tests where membrane force (
) dominates the maximum stress.
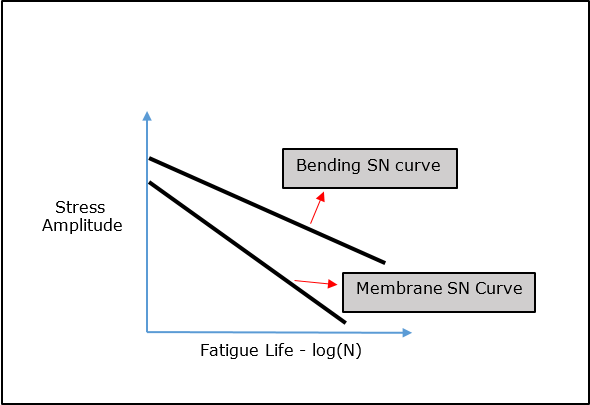
Figure 27: Example Stress Amplitude vs Fatigue Life log(N) for Bending dominated vs Membrane Dominated structure.
The upper and lower curves are referred to as Bending SN curve and Membrane SN curve, respectively. It is recommended that membrane SN curve should be used when membrane stress dominates in an element, and bending SN curve should be used when bending stress dominates. Interpolation between the two curves may be carried out depending on the degree of bending dominance.
Degree of bending dominance can be determined by the average bending ratio (
). First, the bending ratio (r) is defined as:
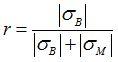
Where,
is the maximum bending stress equal to 
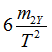
is the maximum membrane stress equal to 
The average bending ratio (
) for an element is defined as:
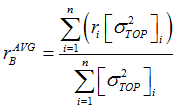
Where
is the square of the maximum stress at the top surface of shell element i at which the damage is calculated (that is, root, toe, or throat shell elements).
ri is the bending ratio of shell element i.
An interpolation factor (IF) is now defined as:
IF=0.0 w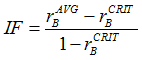hen 
when 
The 
value is defined by the BRATIO field on the PFATSMW Bulk Data Entry. It is set to 0.5 by default. If average bending ratio (
) is less than or equal to the critical bending ratio (
), then the Membrane SN curve is used to assess damage. If average bending ratio is greater than the critical bending ratio, then an SN curve that is interpolated between membrane SN curve and the bending SN curve is used. The value of the interpolation factor (IF) is used in the linear interpolation method as illustrated in Figure 28. For example, if you consider the Fatigue Strength coefficient value (SR1_i) for the interpolated curve, the calculation is performed as:
SR1_i = [SR1_m + (SR1_b – SR1_m) IF]
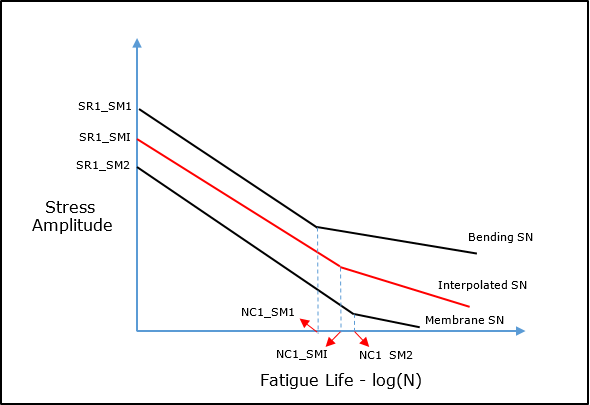
Figure 28: Example Stress Amplitude vs Fatigue Life log(N) for Bending dominated vs Membrane Dominated structure.
The thickness correction process is for size effect correction. SN curves are based on test results from a particular size of the specimen. In reality, the stress vs life curve may vary depending on specimen size. Therefore, thickness correction parameters can be used to correct for this effect. It may be applied based on the thickness T of each shell element under consideration for Fatigue calculation (that is, toe, root, or throat element). The calculations are:
If T ≤ TREF, then there is no Thickness Correction.
If T > TREF, OptiStruct increases stress based on the equation below:
This results in fatigue life reduction, making the design more conservative. TREF and TREF_N can be defined via the corresponding fields on the PFATSMW bulk data entry. The default values are 1.0 and 0.2 respectively. The defaults are in inches (English units), if the metric system is used, then the values should be modified accordingly.
Thickness Correction can be turned on or off using the corresponding THCKCORR field on the FATPARM bulk data entry for Seam Weld Fatigue Analysis.
FKM mean stress correction is supported for Seam Weld Fatigue. Stress sensitivity can be defined on the MATFAT bulk data entry via the FKMMSS_SM field. Mean stress correction for Seam Weld fatigue is disabled by default and can be enabled via the corresponding CORRECT field on the FATPARM bulk data entry.
To activate Seam Weld Fatigue Analysis, FATDEF has to have an FATSEAM and PFATSMW identifier.
| 1. | The FATDEF Bulk and Subcase entries can be used to identify the elements for which fatigue analysis should be performed. For seam weld fatigue, the FATSEAM and PFATSMW entries should be referenced on the FATDEF entry. The FATSEAM entry identifies the corresponding shell elements (CQUAD4 and CTRIA3) for which fatigue analysis is to be performed. |
| 2. | The FATDEF Bulk Data Entry also provides the corresponding PFATSMW Bulk Data Entry references for each FATSEAM entry set to define the seam weld fatigue properties. |
| 1. | The FATPARM Bulk and Subcase entries can be used to specify fatigue parameters for the seam weld fatigue analysis. |
| 2. | The SMWLD continuation line on the FATPARM entry allows you to input the seam weld fatigue method and identify various parameters. |
| 3. | The PFATSMW Bulk Data Entry allows the definition of some properties for seam weld fatigue analysis. |
| 1. | The MATFAT Bulk Data Entry can be used to specify the material properties for seam weld fatigue analysis. |
| 2. | The SMWLD continuation line allows you to specify mean stress sensitivity value, and separate SN curve attributes for bending and membrane SN curves. Bending SN curve and membrane SN curve may be defined in MATFAT after a flag SMWLD. If only one SN curve is defined for seam weld, it is used as both bending SN curve and membrane SN curve. |
| 1. | Similar to regular fatigue analysis, the FATLOAD, FATSEQ, and FATEVNT entries can be used to define loading sequences. |
| 1. | The PTYPE field on the DRESP1 entry can be set to FATSEAM and the ATTi fields should be FATSEAM identification numbers for seam weld fatigue optimization. |
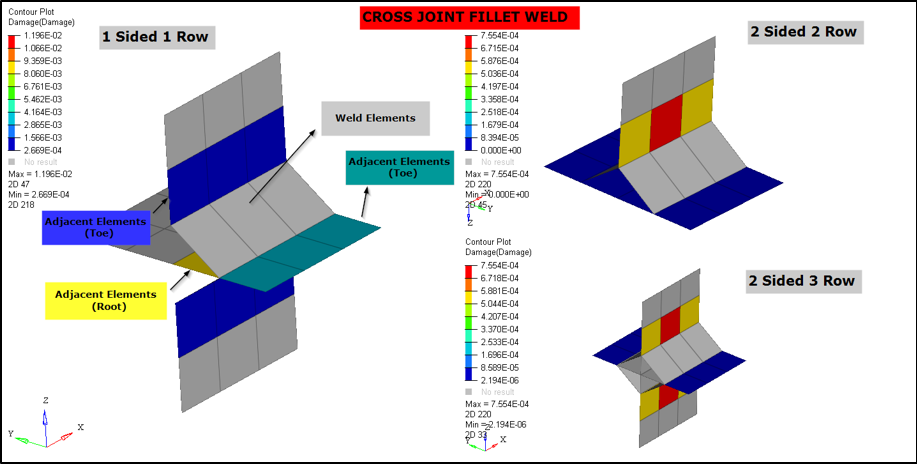
Figure 29: Example Cross Joint Fillet Weld Output for Damage
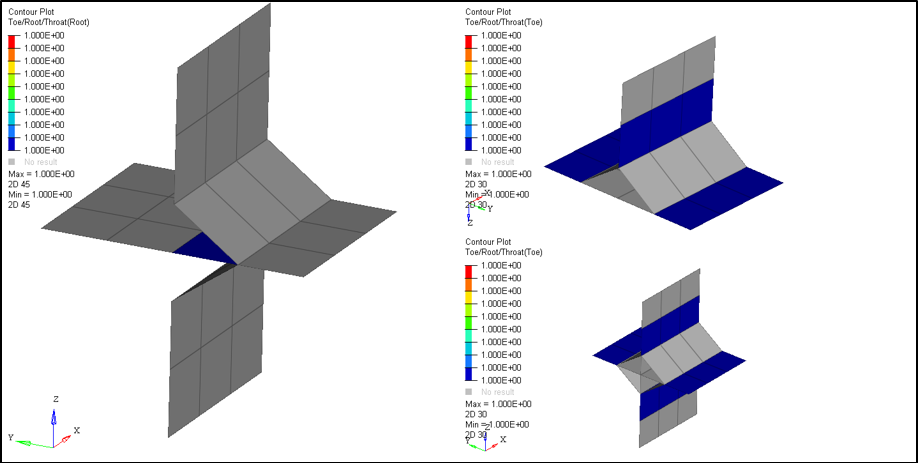
Figure 30: Example Cross Joint Fillet Weld Output for Toe/Root/Throat elements
See Also:
