Springs |

|

|

|

|
|
Springs |

|

|

|

|
Pretensioner spring type 32 and multi-strand spring type 28 are discussed here. For further information, refer to the RADIOSS Theory Manual.
The relation between force and displacement is completely user-defined. Several formulations are available to define the stiffness evolution. It is also possible to add viscous effects by considering damping. The formulation does not have to be the same for all DOF's.
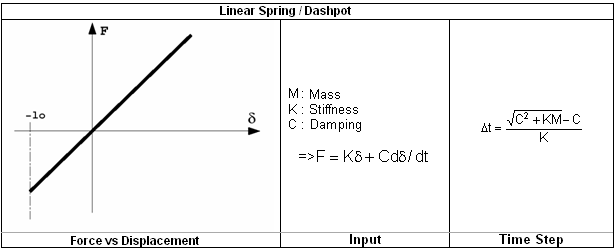
The simplest formulation enables you to model linear elastic spring where the internal force is proportional to the relative displacement.
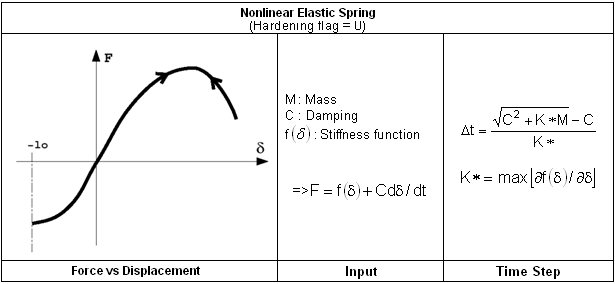
The nonlinear elastic model is similar to the linear model; except that the stiffness is no longer constant. A function must be defined that relates the Force to the Displacement. As the model is elastic, the loading and unloading follow the same path.
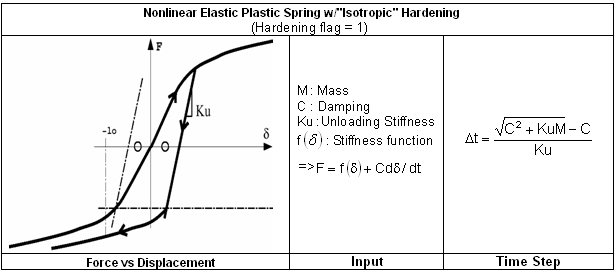
Permanent deformation can also be modeled with the nonlinear elasto-plastic formulation. Note that the unloading stiffness (Ku) may be different than the loading stiffness (K).
|
The following formulation, contrary to the previous one, enables you to uncouple the tensile and compression behavior.
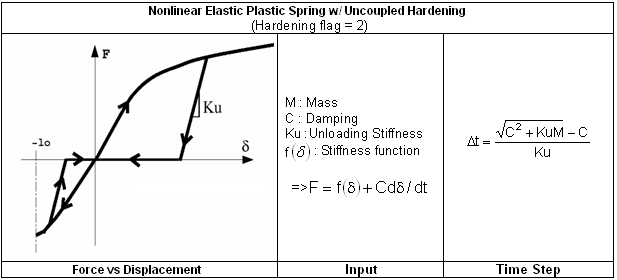
If the minimum and maximum yield curves have identical shapes, the hardening is considered to be kinematic, as follows:

The nonlinear elastic-plastic spring with nonlinear unloading allows you to model uncoupled hardening in compression and tensile behavior with nonlinear unloading.
The unloading is defined by:
![]()
with, ![]()
Where ![]() and n being computed using K and F(
and n being computed using K and F(![]() max).
max).
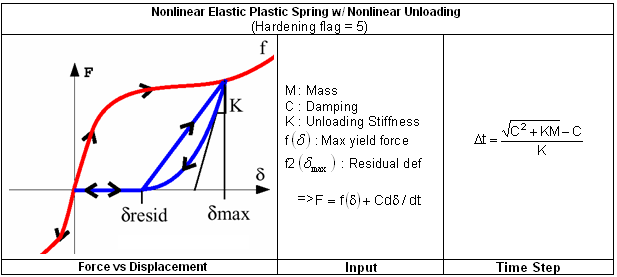
Uncoupled hardening in compression and tensile behavior with nonlinear unloading. The unloading is defined by:
![]()
with, ![]()
Where, ![]() and n being computed using K and F(
and n being computed using K and F(![]() max).
max).
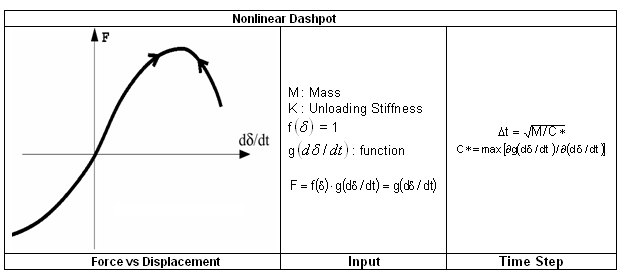
To simplify, in the previous cases the damping was considered as linear, but it is possible to use nonlinear damping.
When creating a spring property with a user-defined curve “Force vs Displacement” for the stiffness, typically the end of the curve has a very high slope to deal with very high compression. In this case, the following warning is often received with RADIOSS Starter.
WARNING ID: 506 ** WARNING IN SPRING PROPERTY ** WARNING IN SPRING PROPERTY SET ID=XXX STIFFNESS VALUE 100 IS NOT CONSISTENT WITH THE MAXIMUM SLOPE (4550) OF THE YIELD FUNCTION ID=X THE STIFFNESS VALUE IS CHANGED TO 1000 |
This warning comes from the fact that the slope of the input curve (the stiffness) is not consistent with the initial stiffness. If the maximum slope of the curve (the maximum stiffness) is greater than the initial stiffness, unloading in the zone of maximum slope will be false (Fig. 3.15). To obtain proper behavior, RADIOSS Starter modifies the initial stiffness according to the maximum slope.
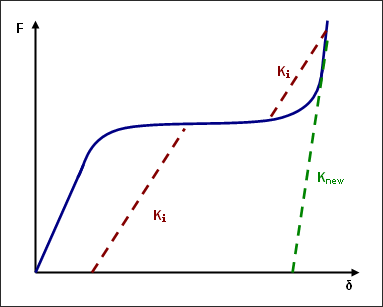
Fig. 3.15: Stiffness not consistent
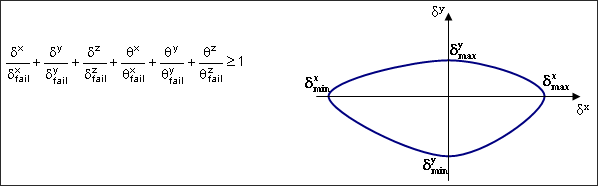
Several rupture criteria for spring elements based on displacement, force or internal energy are available in RADIOSS. Rupture criteria can be uni-directional or multi-directional. If the criteria is uni-directional, the spring will fail as soon as the criteria is satisfied for one degree of freedom:
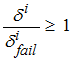
Where, i is any degree of freedom.
Whereas, if the criteria is multi-directional, all degrees of freedom are coupled to determine failure:
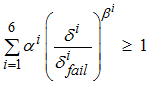
This criteria was the first to be implemented in RADIOSS. This one is very easy to input, the maximum allowable displacement for each degree of freedom is defined. For multi-directional criteria, ![]() i and
i and ![]() i are set to 1 and 2, respectively; therefore, the spring will fail as soon as the following criteria is reached:
i are set to 1 and 2, respectively; therefore, the spring will fail as soon as the following criteria is reached:
New failure criteria will allow model velocity dependent rupture limits, they are available with displacement, force and internal energy. Therefore, ![]() fail is modified as follows to take into account the velocity:
fail is modified as follows to take into account the velocity:
| • | For translational DOF |
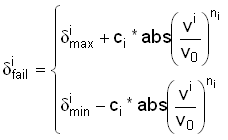
| • | For rotational DOF |
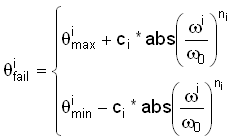
The above formula's are valid for displacement/rotation, force/moment and energy.