16.1 - EXPLICIT Solver |

|

|

|

|
|
16.1 - EXPLICIT Solver |

|

|

|

|
TitleEXPLICIT solver |
|
||||||||||||||||
Number16.1 |
|||||||||||||||||
Brief DescriptionA dummy is sat down via gravity using the quasi-static load treatment. |
|||||||||||||||||
Keywords
|
|||||||||||||||||
RADIOSS Options
|
|||||||||||||||||
Input FileRayleigh_damping: <install_directory>/demos/hwsolvers/radioss/16_Dummy_Positioning/EXPLICIT_solver/RAYLEIGH/.../SEAT_RAYLEIGH* Dynamic_relaxation: <install_directory>/demos/hwsolvers/radioss/16_Dummy_Positioning/EXPLICIT_solver/DYREL/SEAT_DYREL* Kinetic_relaxation: <install_directory>/demos/hwsolvers/radioss/16_Dummy_Positioning/EXPLICIT_solver/KEREL/SEAT_KEREL* Without_damping: <install_directory>/demos/hwsolvers/radioss/16_Dummy_Positioning/EXPLICIT_solver/Without_damping/SEAT* |
|||||||||||||||||
Technical / Theoretical LevelAdvanced |
|||||||||||||||||
The topic of this study concerns quasi-static load treatment using kinetic relaxation, dynamic relaxation and Rayleigh damping. The explicit solutions provided by the three different approaches will be compared and analyzed.
The purpose is to position a dummy on a foam seat under the gravity field using a quasi-static approach prior to a possible dynamic crash simulation.
Units: mm, s, ton, N, MPa
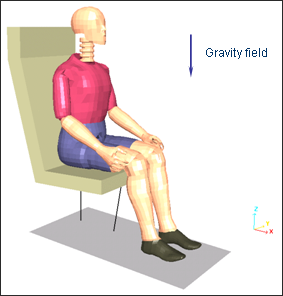
Fig 1: Problem studied.
The dummy weighs 80 kg (173.4 lbs.). The material introduced does not represent the physical case; however, the global weight of the dummy is respected. As the dummy deformation is neglected in this loading phase, simplifying the material characterizations has no incidence on the simulation.
Material for seat brace - both the columns and the floor are made of steel with the following properties (/MAT/LAW1):
| • | Young’s modulus: 210000 MPa |
| • | Poisson’s ratio: 0.3 |
| • | Density: 7.8 x 10-9 Gkg/l |
The seat columns have the following characteristics:
| • | Area: 2580 mm2 |
| • | Inertia: IXX = 554975 mm4; IYY = 554975 mm4; IZZ = 937908 mm4 |
The thickness for the seat back and the floor:
| • | Brace thickness = 2 mm |
| • | Floor thickness = 1 mm |
The seat cushion is made of foam which can be described using the generalized Kelvin-Voigt model. The material properties of the foam are:
| • | Young’s modulus: 0.2 MPa |
| • | Poisson’s ratio: 0 |
| • | Density: 4.3 x 10-11 Gkg/l |
| • | E1 and E2: 0 MPa |
| • | Tangent modulus: 0.25 MPa |
| • | Viscosity in pure shear: 10000 MPa/s |
| • | C1 = C2 = C3 = 1 (visco-elastic bulk viscosity) |
RADIOSS material law 35 is used. The open cell foam option is not active (IFlag = 0) and the pressure is read using the following input curve:
Table 1: Pressure versus compression curve.
Compression |
-100000 |
-10 |
0 |
3000 |
209000 |
210000 |
Pressure |
-1000 |
-1000 |
0 |
7.633 |
7.633 |
18.5 |
Based on the Navier equation, law 35 describes materials using visco-elastic behavior. The effect of the air enclosed is taken into account via a separate pressure versus compression function. Relaxation and creep can be modeled.
The schematic model in Fig 2 describes the generalized Kelvin-Voigt model where a time-dependent spring working in parallel with a Navier dashpot is put in a series with a nonlinear rate-dependent spring.
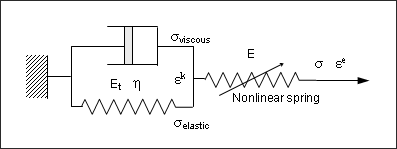
Fig 2: Generalized Kelvin-Voigt model – Law 35.
Two pressure computations are available in RADIOSS for foam having no open cells. The expression used by default is:
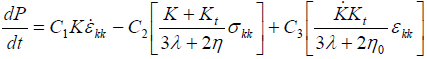
See the RADIOSS Theory Manual for explanation of coefficients.
Pressure may also be computed using the pressure versus compression curve defined by you. The compression, u is defined as:
![]()
Where, ![]() is the density at a time t, and
is the density at a time t, and ![]() 0 is the initial density.
0 is the initial density.
The model consists of two subsets:
| • | a dummy composed of 38 parts (limbs and joints). |
| • | a seat comprised of six parts (foam seat back, foam seat cushion, seat back brace, seat bottom brace, seat columns and the floor). |
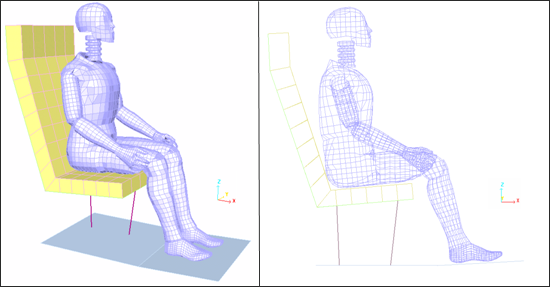
| Fig 3: Model mesh. | Fig 4: Model mesh. |
| (Perspective view – Shaded display) | (Profile view – Edges display) |
The seat cushion is meshed with 70 brick elements defined by general type 14 solid property.
| • | Quadratic bulk viscosity: 1.1 |
| • | Linear bulk viscosity: 0.05 |
| • | Hourglass viscosity coefficient: 0.1 |
The dummy and seat brace are modeled with shell elements, divided into 4871 4-node shells and 203 3-node shells (Dummy: 5004 shells and seat: 70 shells).
Using a dummy in the model, the /DEL/SHELL/1 option should be activated in the Engine file to avoid a small time step, due to the low density of material defining the dummy envelope.
The shell properties are:
| • | Belytschko hourglass formulation (Hourglass type 4, Ishell = 4). |
| • | Membrane hourglass coefficients: 0.01 (default value) |
| • | Out-of-plane hourglass: 0.01 (default value) |
| • | Rotation hourglass coefficient: 0.01 (default value) |
Contacts between the dummy and the seat cushion, as well as between the foot and the floor, use type 7 interface models with the penalty method. Additionally, symmetrical contact between the body and seat is achieved by creating two complementary interfaces, as shown below:
First interface: Dummy parts: slave nodes
Seat: master surface
Second interface: Dummy parts: master surface
Seat: slave nodes
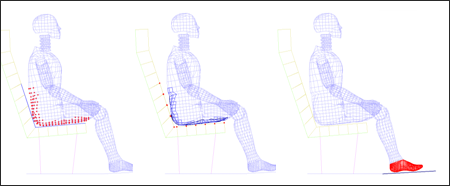
Fig 5: Contacts modeling with type 7 symmetrical interface
The gap between the symmetrical interfaces is equal to 5 mm, while a gap of 0.5 mm is set for the other interface.
The type 7 interface allows sliding to occur between surfaces. A Coulomb friction can be introduced; in addition, a critical viscous damping coefficient can be defined to damp sliding.
The symmetric interfaces properties are:
| • | Coulomb friction (Fric flag) = 0.3 |
| • | Critical damping coefficient (Visc flag) = 0.05 |
| • | Scale factor for stiffness (Stfac flag) = 1 |
| • | Sorting factor (Bumult flag) = 0.20 |
See the RADIOSS Theory Manual and Starter Input for further information about the definition of the type 7 interface.
The goal is to set the body on the seat using a quasi-static approach in order to obtain static equilibrium. The positioning phase is not included in this study. Thus, all nodes of the dummy are placed in a global rigid body in order to maintain the dummy’s initial configuration.
In order to save the CPU, a second global rigid body includes parts of the seat and the floor; except for the seat cushion parts, which will only have active elements during simulation.
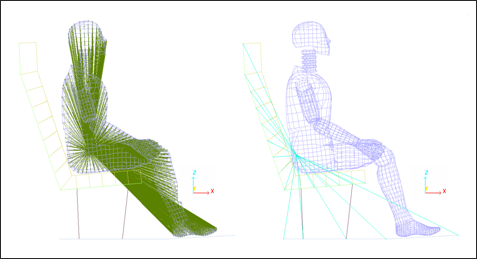
Fig 6: Set up of both rigid bodies.
When the ICoG flag is set to 1 for the rigid body of the seat, the center of gravity is computed using the master and slave node coordinates, and the master node is moved to the center of gravity, where mass and inertia are placed.
When the ICoG flag is set to 3 for the rigid body of the dummy, the center of gravity is set at the master node coordinates defined by you. The added masses and added inertia are transmitted to the master node coordinates.
The master node coordinates and skew are extracted from the pelvis part of the original rigid body.
Gravity is applied to all nodes of the model. A function defines gravity acceleration in the z direction versus time. Gravity is activated by /GRAV in the Starter file (*_0000.rad).
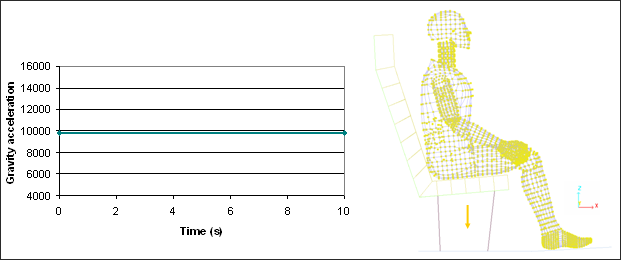
Fig 7: Input gravity function (-9810 mm.s-2) and nodes selection (yellow).
The six rigid body modes of the seat are removed by completely fixing the rigid body master node attached to the seat. In order to limit the out-of-plane vibrations, the master node of the dummy's rigid body is fixed in translation along the Y axis.
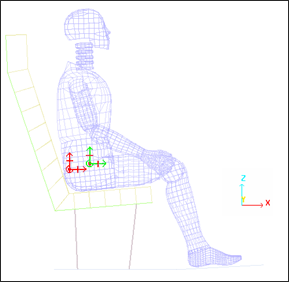
Fig 8: Boundary conditions on the rigid bodies’ master nodes.
Static analysis: quasi-static treatment of gravity loading up to static equilibrium.
The explicit time integration scheme starts with nodal acceleration computation. It is efficient for simulating dynamic loading. However, a quasi-static simulation via a dynamic resolution method needs to minimize the dynamic effects in order to converge towards static equilibrium. This usually describes the pre-loading case prior to dynamic analysis. Thus, the quasi-static solution of gravity loading on the model is the steady state part of the transient response.
To reduce the dynamic effect, three options are available in the Engine file:
| • | Kinetic relaxation (/KEREL) |
| • | Dynamic relaxation (/DYREL) |
| • | Rayleigh damping (/DAMP) |
All velocities are set to zero each time the kinetic energy reaches a maximum value. This option is activated in the Engine file using /KEREL (input is not required).
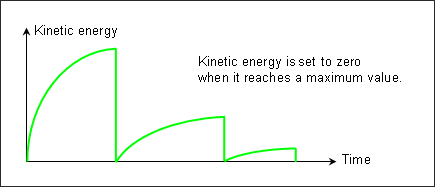
Fig 9: Kinetic relaxation method with /KEREL (also named energy discrete relaxation).
Dynamic loading is damped by introducing a diagonal damping matrix, proportional to mass matrix, in the dynamic equation:
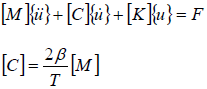
with, ![]() being the relaxation value (recommended default value 1), and T being the period to be damped (less than or equal to the highest period of the system).
being the relaxation value (recommended default value 1), and T being the period to be damped (less than or equal to the highest period of the system).
Thus, a viscous stress tensor is added to the stress tensor:
![]()
Using an explicit code, application of the dashpot force reduces the velocity equation modification:
![]()
![]()
This option is activated in the Engine file (*_0001.rad) using /DYREL (inputs: ![]() and T ).
and T ).
Dynamic loading is damped by introducing a damping matrix, proportional to the mass and stiffness matrix, in the dynamic equation. This simplified approach will allow you to reduce the global equilibrium equation to n-uncoupled equations by using an orthogonal transformation. This damping is said to be proportionally uncoupled.
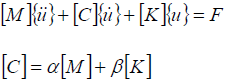
Where, a and ![]() are the pre-defined constants.
are the pre-defined constants.
The orthogonal transformation using this proportional damping assumption leads to:
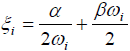
| with, |
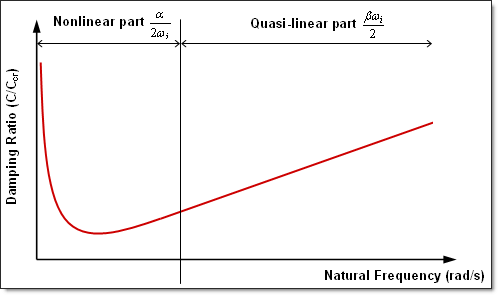
Fig 10: Rayleigh type damping.
If you have some experimental results, the proportionality factors, a and ![]() are found by evaluating the damping for a pair of the most significant frequencies used. Thus, two equations with two unknown variables are obtained:
are found by evaluating the damping for a pair of the most significant frequencies used. Thus, two equations with two unknown variables are obtained:
![]()
If several frequencies are available, an average of computed values, a and ![]() may be used.
may be used.
This model of proportional damping is not recommended for complex structures and does not enable good experimental retiming.
This option is activated in the Engine file (*_0001.rad) using /DAMP (inputs data: a and ![]() ).
).
In this example, a and ![]() are set to the following values:
are set to the following values:
| • | First case: a = 10 and |
| • | Second case: a = 0 and |
| • | Third case: a = 10 and |
| • | Fourth case: a = 20 and |
The resulting assumptions are:
| • | First case: [C] = 10[M] + 10[K] |
| • | Second case: [C] = 10[K] |
| • | Third case: [C] = 10[M] |
| • | Fourth case: [C] = 20[M] |
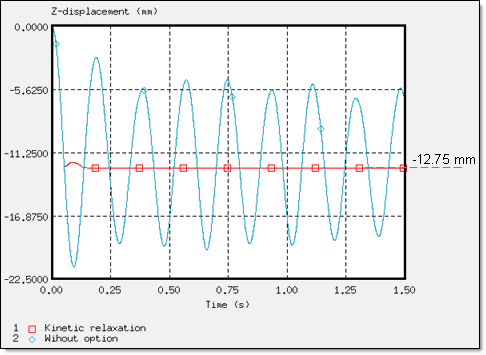
Fig 11: Z-displacement of the rigid body’s master node on dummy (node 14199).
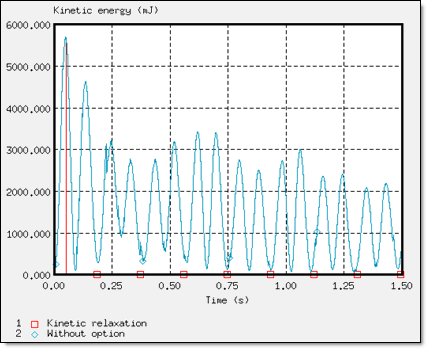
Fig 12: Kinetic energy of global model.
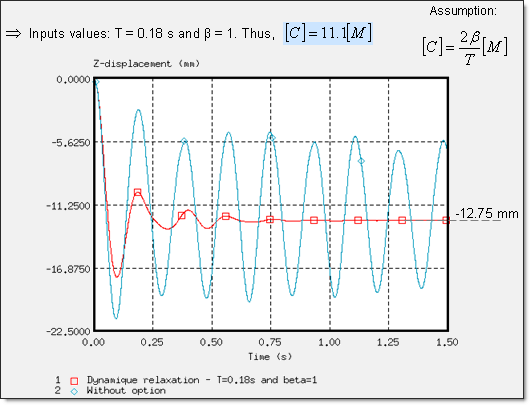
Fig 13: Z-displacement of the rigid body’s master node on dummy (node 14199).
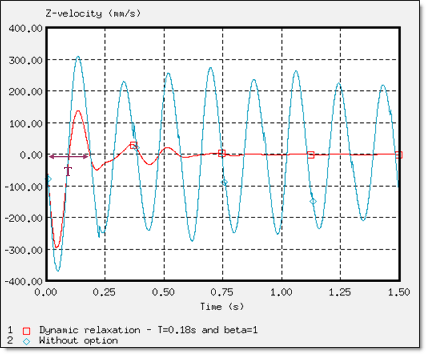
Fig 14: Z-velocity of the rigid body’s master node on dummy (node 14199).
The period T to be damped is estimated from the velocity curves (highest period).
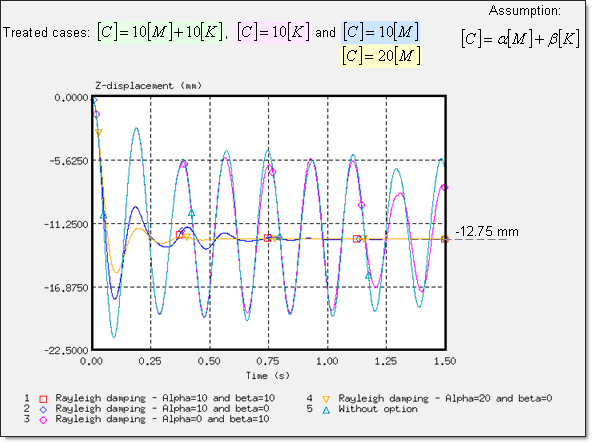
Fig 15: Z-displacement of the rigid body’s master node on dummy (node 14199)
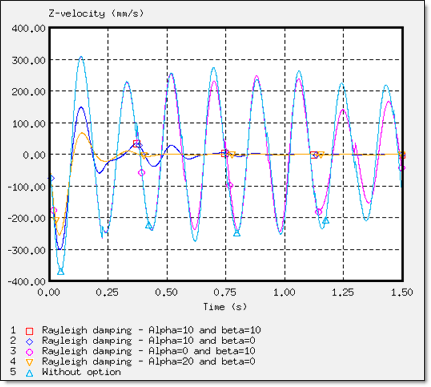
Fig 16: Z-velocity of rigid body’s master node on dummy (node 14199)
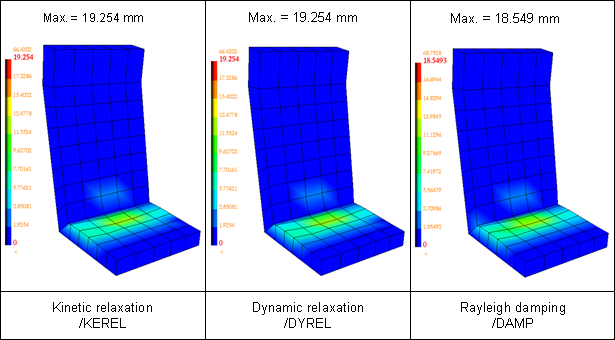
Fig 17: Comparison of the nodal displacements’ display on the seat at time t = 1.48 s
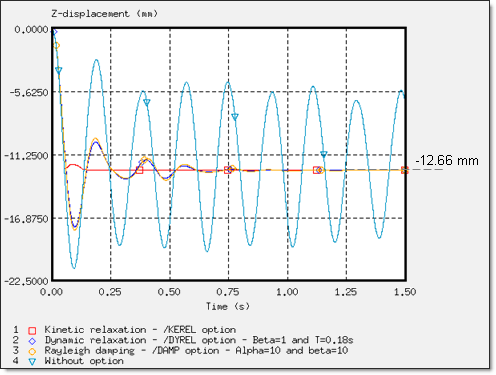
Fig 18: Comparison of damping on displacement obtained using the three static approaches
(Z-displacement of the rigid body’s master node on dummy: node 14199)
It is undeniable that the damping methods used to converge towards static equilibrium provide accurate results, especially in the case of this problem where the low rigidity of the seat caused very little quenched oscillations.
The kinetic relaxation introduced in /KEREL, was relatively effective having a swift convergence of the solution towards a static solution, in addition to being easy to use since no input is required. Stability was obtained at 0.137 s.
The /DYREL and /DAMP options are based on viscous damping conducted for the same response, with convergence in three oscillations. Stability was obtained at 0.75 s. Furthermore, dynamic relaxation and the Rayleigh damping methods are basically equivalent in this problem, due to the low stiffness of the seat cushion (Young’s modulus is equal to 0.2 MPa), which breaks the balance between the mass and the weight stiffness in the Rayleigh assumption. Moreover, the boundary conditions and the loading applied on the model lead to a problem described using a predominant natural frequency. Thus, only one parameter, a is needed to describe this physical behavior, which reverts back to the dynamic relaxation assumption.
Using ![]() =1 and T =0.18s for dynamic relaxation and
=1 and T =0.18s for dynamic relaxation and ![]() =10 for Rayleigh damping, you achieve:
=10 for Rayleigh damping, you achieve:
| • | Dynamic relaxation: |
![]()
| • | Rayleigh damping: |
[C] = ![]() [M] +
[M] + ![]() [K] ≈
[K] ≈ ![]() [M]
[M]
≈ 10[M]
In conclusion, the approaches available in RADIOSS provided after convergence a single solution, namely displacement of the dummy by -12.66 mm along the Z-axis and an identical deformation of the seat cushion.