Overview

---

Aim of the Problem

The purpose of this example is to investigate the transmission of momentum between several balls. Contact with the various interfaces using the Penalty and Lagrange Multipliers’ method is analyzed.

Physical Problem Description

Pool is a game consisting of 16 balls, each 50.8 mm in diameter. It is played on a small billiard table measuring 1800 mm x 900 mm. Fifteen (15) balls are placed in a triangle to enable their tight grouping. The initial velocity of the shooting (cue) ball is presumed equal to 1.5 ms-1. Elastic rebounds are observed.

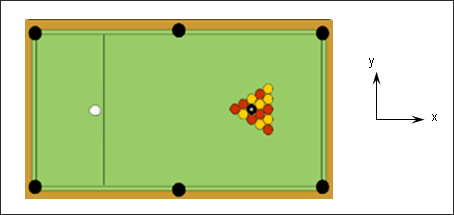
Fig 1: Pool game.

Units: mm, g, N, MPa.

The material is subjected to a linear elastic law (/MAT/LAW1) with the following properties:

 

Analysis, Assumptions and Modeling Description

---

Modeling Methodology

The balls are meshed with 16–node solid shells (quadratic elements) in order to improve the conditions of contact by taking into account the curvatures. The frame of the table is made of 16–node solid shells to comply with the interface used. The plate is modeled using only one solid element. The 16–node thick shells are considered as solid elements. They are defined by a thick type 20 shell property (number 16 solid formulation for quadratic 16-node thick shells, fully-integrated with 2x2x2 integration points).

Fig 2: Pool game mesh.

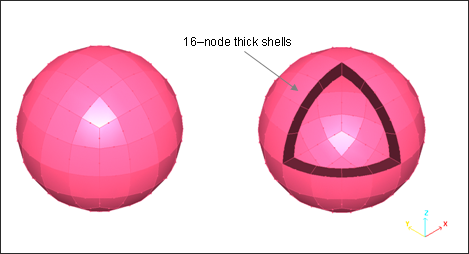
Fig 3: Mesh for balls.

Fig 4: 16-node thick shell element.

The type 16 interface with the Lagrange Multipliers method is used to model the ball/ball and balls/table contacts. An interface must be defined for each ball (that is: 16 interfaces in total). An additional interface is used to define the contacts between the balls and the table (plate and frame).

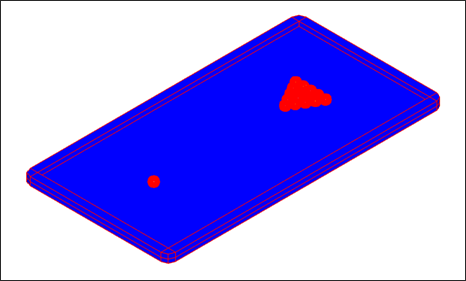
Fig 5: Type 16 interface: slave SHEL16 for balls and master SHEL16 for the table.

Fig 6: Example of the type 16 interface defined for the contact between balls.

Slave nodes (red) are extracted from the external surfaces of the parts.

RADIOSS Options Used

An initial velocity of 1.5 ms-1 in X direction is applied to all nodes of the white (cue) ball.

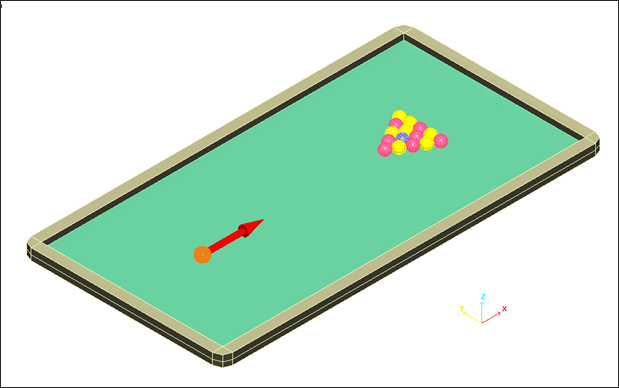
Fig 7: Initial translational velocities of the impacting ball.

All nodes of the lower face of the table are completely fixed (translations and rotations).

Gravity is considered for all the balls nodes. A function defines the gravity acceleration in the Z direction compared with time. Gravity is activated using /GRAV.

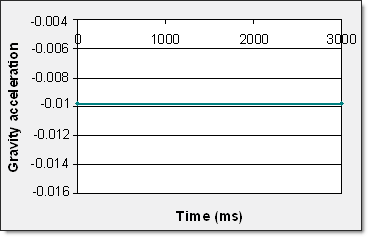
Fig 8: Gravity function (-0.00981 mm.ms-2 )

Simulation Results and Conclusions

---

Curves and Animations

Due to the faceting of the ball, contact between the impacting ball and the impacted balls is not perfectly symmetrical and momentum is not homogeneously transmitted among the balls.  An apparent physical strike thus results.

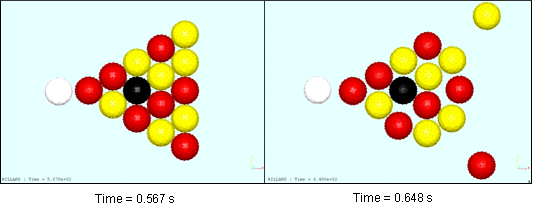
Fig 9: Collision of the balls

Fig 10: History of the balls’ motions (contact control: type 16 interface).