CORD2S

Bulk Data Entry

CORD2S – Spherical Coordinate System Definition, Form 2

Description

This entry defines a spherical coordinate system three grid points. The coordinates of the three non-collinear grid points are used to uniquely define the coordinate system. The first point defines the origin. The second point defines the direction of the Z-axis. The third lies in the X-Z plane (see Figure 1).

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
CORD2S	CID	RID	A1	A2	A3	B1	B2	B3
	C1	C2	C3

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
CORD2S	3		-2.9	1.0	0.0	3.6	0.0	1.0
	5.2	1.0	-2.9

Field	Contents
CID	Unique coordinate system identification number. (Integer > 0)
RID	Identification number of a coordinate system that is defined independently from this coordinate system (see comment 7). Default = 0 (Integer > 0)
A1,A2,A3 B1,B2,B3 C1,C2,C3	Coordinates of three points in the reference coordinate system (RID). If RID is blank or 0, the reference coordinate system is the default basic coordinate system. (Real)

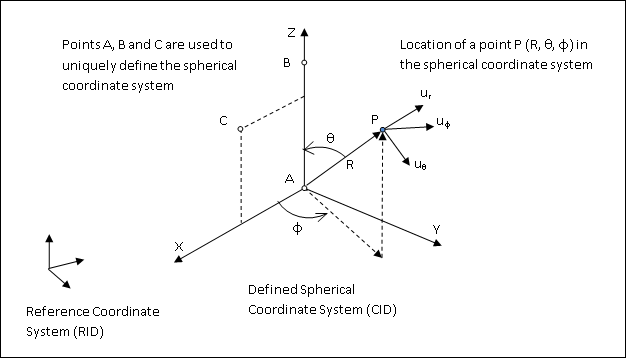
cord2s

Figure 1: Defining a Spherical Coordinate System (CID) using grid points A, B and C.

Comments

1.	The three points (A1, A2, and A3), (B1, B2, and B3), and (C1, C2, and C3) must be unique and non-collinear. Non-collinearity is checked by the geometry processor.

2.	Coordinate system identification numbers on all CORD1R, CORD1C, CORD1S, CORD2R, CORD2C, CORD2S, CORD3R, and CORD4R entries must all be unique.

3.	A duplicate identification number is allowed if the CID and GID are identical and the coordinates are within the value set by PARAM, DUPTOL (see Guidelines for Bulk Data Entries for further information).

4.	The location of a grid point (P in Figure 1) in this spherical coordinate system is given by (R, θ, and ). Where, θ and are measured in degrees.

5.	The displacement coordinate directions at P are (ur, uθ, and u) as shown in Figure 1. The displacements in all three of these directions at the grid point are specified in units of length.

6.	Points on the polar axis may not have their displacement directions defined in this coordinate system due to ambiguity.

7.	The reference coordinate system (RID) should be independently defined or left blank. If blank (or 0), the reference coordinate system is the default basic coordinate system. In such cases, A, B and C are defined with respect to the basic coordinate system.

8.	This card is represented as a system in HyperMesh.