Example 21 - Cam |

|

|

|

|
|
Example 21 - Cam |

|

|

|

|
A cam can be considered as a device that translates motion from circular to linear. The camshaft of a car takes the rotary motion of the engine and translates it into the linear motion required for operating the intake and exhaust valves.
The purpose of this example is to illustrate the capacity of RADIOSS to simulate the dynamic behavior and the kinematic motion of a cam-valve system. The smooth motion of the valve can be simulated using an adequate and accurate contact model having contact algorithms with quadratic surfaces without any gaps.
TitleCam |
|
||||||||||
Number21.1 |
|||||||||||
Brief DescriptionThe modeling of a camshaft, which takes the engine’s rotary motion and translates it into linear motion for operating the intake and exhaust valves, is studied. |
|||||||||||
Keywords
|
|||||||||||
RADIOSS Options
|
|||||||||||
Input FileInterface 16: Fine mesh: <install_directory>/demos/hwsolvers/radioss/21_Cam/interface16/fine_mesh/I16S16FM* Coarse mesh: <install_directory>/demos/hwsolvers/radioss/21_Cam/interface16/coarse_mesh/I16S16CM* Interface 7: Penalty method: <install_directory>/demos/hwsolvers/radioss/21_Cam/interface7/penalty/slave_cam/I7PMCAM* <install_directory>/demos/hwsolvers/radioss/21_Cam/interface7/penalty/slave_valve/I7PMVALVE* Lagrange multipliers: <install_directory>/demos/hwsolvers/radioss/21_Cam/interface7/lagrange/slave_cam/I7LMCAM* <install_directory>/demos/hwsolvers/radioss/21_Cam/interface7/lagrange/slave_valve/I7LMVALVE* Friction: <install_directory>/demos/hwsolvers/radioss/21_Cam/interface7/friction/I7PFMCAM* |
|||||||||||
Technical / Theoretical LevelMedium |
|||||||||||
Modeling a contact between a plane and a curved surface uses a faceted curved surface. Interfaces 7 and 16 are compatible with the geometry of the problem and the faceting, are described and compared.
This problem demonstrates a cam rotating with an angular velocity of 314 rad/s, which interacts and triggers off the translation of a valve tied to two springs. The superposed springs have varying stiffness (spring 1: 30000 N/m and spring 2: 15000 N/m). The springs control the higher and lower rotary frequencies.
| • | The cam is 36 mm in length, with a maximum width of 14 mm and a thickness of 18 mm. |
| • | The valve is 44 mm in diameter, with a thickness of 3 mm (Fig 1). |
| • | The spring is 40 mm in length. |
The following system is used: mm, s, kg, mN , KPa.
The material used for the cam and the valve is steel. It is characterized by the isotropic elasto-plastic material (/MAT/LAW2) and the Johnson-Cook plasticity model, with the following properties:
| • | Initial density: 7.8 x 10-06 Mkg/l |
| • | Young modulus: 2.1 x 10+08 KPa |
| • | Poisson ratio: 0.3 |
| • | Yield stress: 20000 KPa |
| • | Hardening parameter: 40000 KPa |
| • | Hardening exponent: 0.5 |
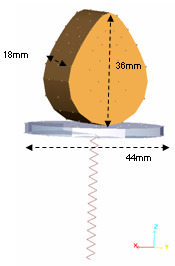
Fig 1: Geometry of the problem.
The problem raised in this example is the modeling of an interface between a plane and a curved surface. In this case, using quadratic elements is the most appropriate.
A type 16 interface with 16-node shell elements for both the valve and the cam should be chosen first for the modeling. 20-node brick elements are used for the mesh inside the cam (Fig 2).
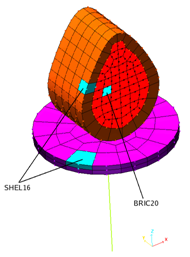
Fig 2: BRIC20 and SHEL16 mesh.
Another model using linear elements is studied. Contact between the cam and valve is defined by a type 7 interface. In order to satisfy the closed contact between parts, the Lagrange Multipliers method is selected.
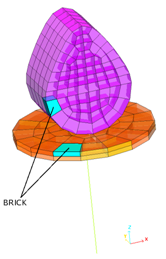
Fig 3: BRICK elements mesh.
The springs are modeled using RADIOSS type 4 springs. The stiffness is linear and defined by the following functions. Damping is neglected.
l-l0 (mm) |
-40 |
0 |
50 |
Fspring 1 (mN) |
-1.5 e+06 |
-0.3 e+06 |
1.2 e+06 |
Fspring 2 (mN) |
-0.75 e+06 |
-0.15 e+06 |
0.6 e+06 |
| • | Rigid bodies: |
In order to apply a constant angular velocity to the cam, a rigid body is created over the internal nodes, as shown in Fig 4. The master node is moved to the camshaft axis.
To attach the valve head to the spring, another rigid body is created to distribute the internal spring force over several nodes.
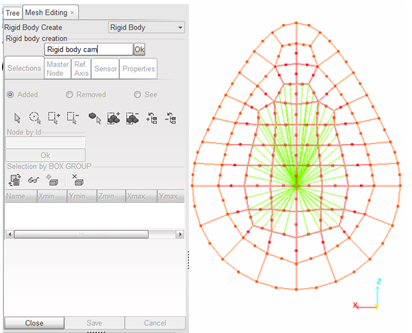
Fig 4: Rigid body cam
| • | Boundary conditions: |
- Master node of the cam is blocked, except when rotating around Y.
- Master node of the valve is blocked, except when translating around Z.
- One extremity of the spring is fixed to the valve, while the other is blocked.
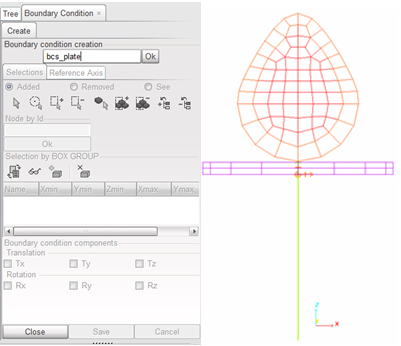
Fig 5: Boundary condition on valve.
| • | Imposed velocity: |
A rotational velocity of 314 rad/s is imposed on the master node of the rigid body. This velocity is activated by a temporal sensor, with a short activation delay (Tdelay =0.0002s). This sensor is necessary to avoid applying the initial and imposed velocities at the same time.
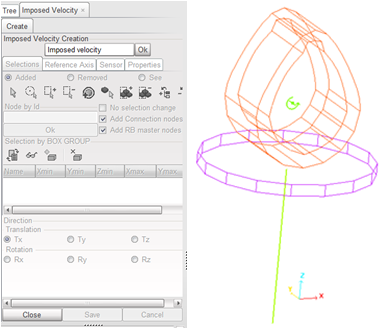
Fig 6: Imposed velocity.
| • | Initial velocity: |
An initial rotational velocity is applied to all the cam’s nodes, including the master node of the rigid body. You must define the origin (center of rotation) and the orientation vector.
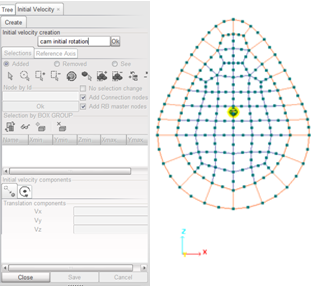
Fig 7: Initial velocity.
| • | Interfaces: |
The type 16 interface simulates a contact between a quadratic master surface and a group of nodes. In the case of contact between a curved and a plane surface, the curved surface is defined as the master surface and the nodes of the plane part are slave.
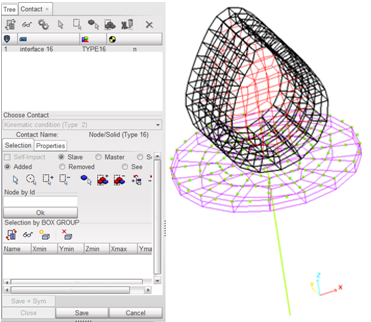
Fig 8: Interface 16.
The type 7 interface works either with Penalty or with Lagrange multipliers. In its basic formulation, the interface simulates contact between two facetisated surfaces. The use of the Lagrange Multipliers method enables to precisely satisfy the kinematic contact without introducing a gap.
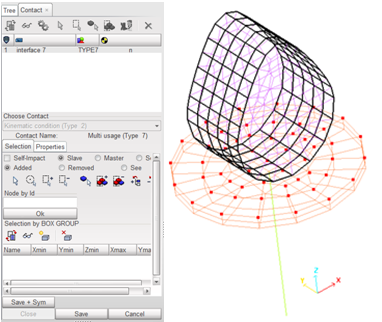
Fig 9: Interface 7.
At first, you are interested by the kinematics of the problem. The results obtained for velocity and acceleration at the master node of the rigid body’s valve are thus compared.
The graphs in Fig 10 provide the velocity of the valve’s master node when a type 7 interface is used with the Penalty method. The raw results obtained are noisy due to the fact that the Penalty method applies discontinued forces. The smooth velocity curve is obtained by using a low pass CFC 180 (3db) filter. Figure 11 shows the acceleration of the same master point.
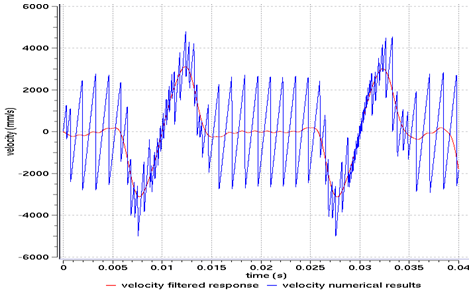
Fig 10: Vertical velocity of the master node valve for a type 7 interface, using the Penalty method.
Attention should be paid to the use of filters. The filtered curves are in fact generally affected by a border effect. Filtering induces an error in the beginning and end parts of the curves (for this example, take the intervals of 0 < t < 0.002 and 0.038 < t < 0.04).
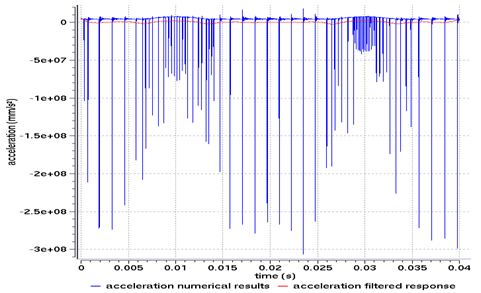
Fig 11: Vertical acceleration of the master node valve for a type 7 interface, using the Penalty method.
The filtering quality depends on the number of samples which, in this case is the number of points computed by RADIOSS for each curve. Therefore, a low value for the /TFILE parameter in the Engine file (*_0001.rad) is used to obtain good results, especially for the acceleration curve.
In the following sections, only the filtered curves are represented in order to the compare different models.
Figures 12 and 13 represent velocity and acceleration curves for a model using a type 7 interface with the Penalty method. As for the master and slave part definition, the results are slightly different.
Figures 14 and 15 give velocity and acceleration curves for type 7 interface using the Lagrange Multipliers method.
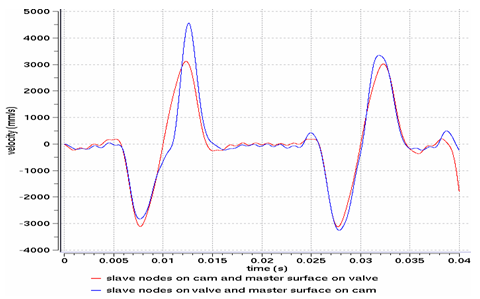
Fig 12: Vertical velocity of the valve’s master node for a type 7 interface, using the Penalty method.
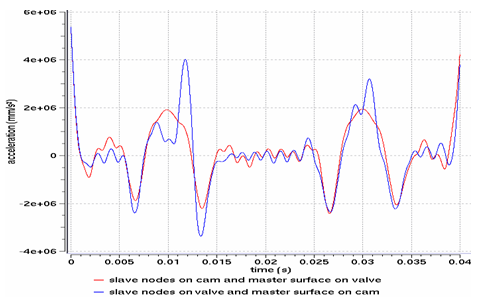
Fig 13: Vertical acceleration of the valve’s master node for a type 7 interface, using the Penalty method.
For both Figures 12 and 13, the model using slave nodes on the cam and a master surface on the valve seems to be the most realistic.
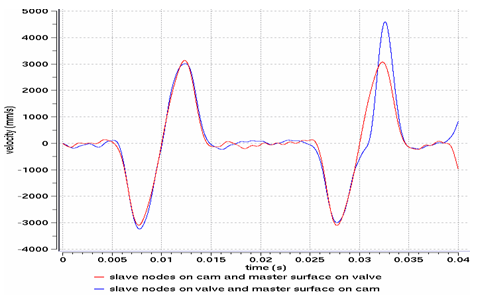
Fig 14: Vertical velocity of the valve’s master node for a type 7 interface, using the Lagrange Multipliers method.
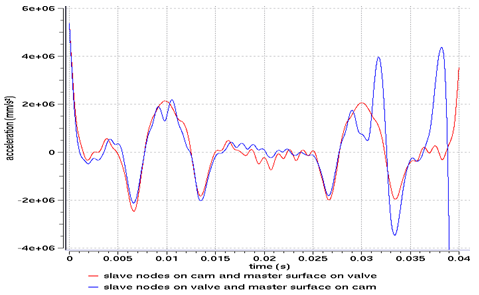
Fig 15: Vertical acceleration of the valve’s master node for a type 7 interface, using the Lagrange Multipliers method.
Even if using a type 7 interface with the Penalty or the Lagrange Multipliers method good results can be achieved, a quadratic mesh with the type 16 interface will enable the reduction of oscillations, due to facetisation.
Figures 16 and 17 compare the results for models using type 7 and 16 interfaces.
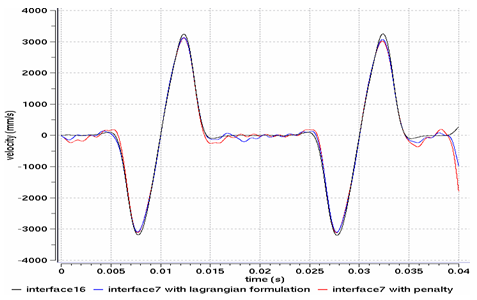
Fig 16: Vertical velocity of the valve’s master node.
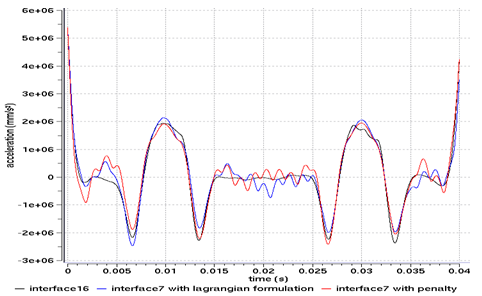
Fig 17: Vertical acceleration of the valve’s master node.
Considering a contact modeled with a type 16 interface, the influence of the mesh density is studied using two relatively coarse and fine meshes
Fine mesh: |
Cam: Valve: |
200 external SHEL16 elements, 250 internal BRIC20 elements 88 SHEL16 elements |
Coarse mesh: |
Cam: Valve: |
40 SHEL16 elements 12 SHEL16 elements |
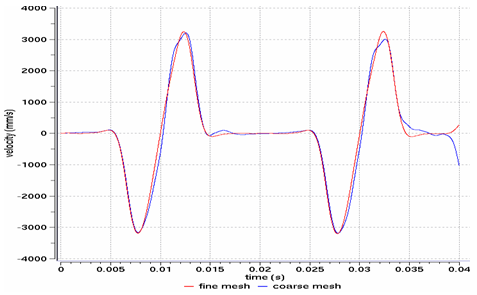
Fig 18: Vertical velocity of the valve’s master node.
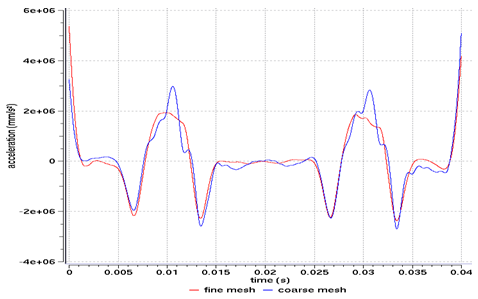
Fig 19: Vertical acceleration of the valve’s master node.
Although the coarser mesh amplifies the facetisation of the curved surfaced, the mesh density does not influence the results for velocity after filtering. However, the fine mesh provides better results for acceleration, having limited parasite oscillations for each node/surface contact.
An option in interface 7 using the Penalty method allows you to add friction to the model. Several friction models are available. The Coulomb friction model is used here. A comparison is made between models with and without friction.
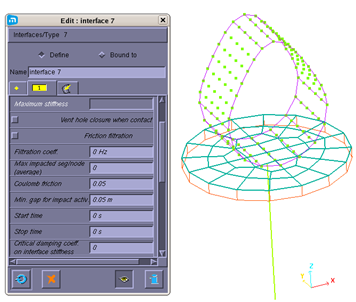
Fig 20: Type 7 interface using Penalty and friction.
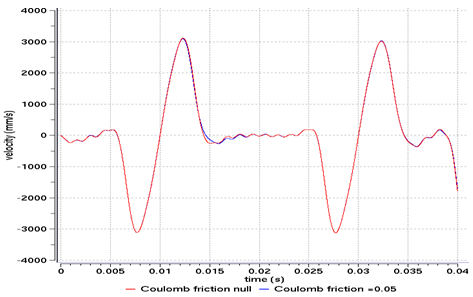
Fig 21: Vertical velocity of the valve’s master node for a type 7 interface, using the Penalty method.
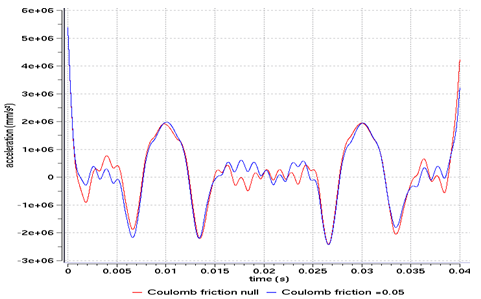
Fig 22: Vertical acceleration of the valve’s master node for a type 7 interface, using the Penalty method.
Simulation |
CPU |
Time Step |
|---|---|---|
Type 16 interface with fine mesh |
22,50 |
0.8365x10-7 |
Type 16 interface with coarse mesh |
1 |
0.207x10-6 |
Type 7 interface with Penalty method (slave nodes on cam and master surface on valve) |
1.65 |
0.2133x10-6 |
Type 7 interface with penalty method (slave nodes on valve and master surface on cam) |
1.75 |
0.2117x10-6 |
Type 7 interface with Lagrange multipliers method |
1.68 |
0.2133x10-6 |
Type 7 interface with Lagrange multipliers method |
1.69 |
0.2126x10-6 |
Type 7 interface with Penalty method and friction |
1.66 |
0.2133x10-6 |
Type 7 interface with Penalty method and friction |
1.65 |
0.2126x10-6 |
This example illustrated the ability of RADIOSS to model mechanisms, particularly in the case of this contact mechanism. Interface types 16 and 7 can be used to model contact between plane and curved surfaces. The type 16 interface enables you to simulate contact between quadratic surfaces without using a gap and provides accurate results within a reasonable computation time. The type 7 interface allows a frictional modeling of the contact, needing little computation time and provides good simulation results.