MAT3

Bulk Data Entry

MAT3 – Material Property Definition, Form 3

Defines the material properties for linear, temperature-independent, and orthotropic materials used by the CTAXI and CTRIAX6 axisymmetric elements.

Format

Field	Contents
MID	Unique material identification number. No default (Integer > 0)
EX, ETH, EZ	Young’s Moduli in the x, θ and z directions, respectively. No default (Real > 0.0)
NUXTH, NUTHZ, NUZX	Poisson’s Ratios: NUXTH = Poisson’s Ratio for strain in the θ direction, when stress in the x direction. NUTHZ = Poisson’s Ratio for strain in the z direction, when stress in the θ direction. NUZX = Poisson’s Ratio for strain in the x direction, when stress in the z direction. No default (Real)
RHO	Mass density. No default (Real)
GZX	Shear Modulus in the x-z plane. No default (Real > 0.0)
AX, ATH, AZ	Thermal expansion coefficient in the x, θ, and z directions, respectively. No default (Real)
TREF	Reference temperature for thermal loading. Default = blank (Real or blank)
GE	Structural element damping coefficient. See comment 6. No default (Real)

1.	The material identification number must be unique for all MAT1, MAT2, MAT8 and MAT9 entries.

2.	Values of all seven elastic constants, EX, ETH, EZ, NUXTH, NUTHZ, NUZX and GZX must be present.

3.	A warning is issued if absolute value of NUXTH or NUTHZ is greater than 1.0.

4.	The x, θ and z directions are principal material directions of the material coordinate system. Each element (that is a CTAXI or CTRIAX6 element) supporting the use of MAT3 contains a “Theta” field to relate the principal material directions to the basic coordinate system.

5.	The strain-stress relationship is:

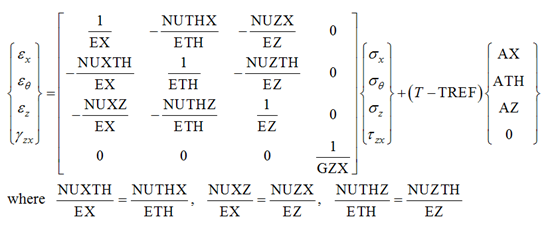
mat3_strain-stress

Note that the strain and stress here are both defined in the material coordinate system.

6.	To obtain the damping coefficient GE, multiply the critical damping ratio, C/C0, by 2.0.

7.	This card is represented as a material in HyperMesh.