MATX62

Bulk Data Entry

MATX62 – Material Property Extension for Hyper-visco-elastic Material for Geometric Nonlinear Analysis

Description

Defines additional material properties for Hyper-visco-elastic material for geometric nonlinear analysis. This material is used to model rubber, polymers, and elastomers. This material is compatible with solid and shell elements.

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MATX62	MID	MUMAX
	LAW	MU1	ALFA1	MU2	ALFA2	MU3	ALFA3
		MU4	ALFA4	MU5	ALFA5	...

Optional continuation lines for Maxwell value:

	MAXWELL	GAM1	T1	GAM2	T2	GAM3	T3
		GAM4	T4	GAM5	T5	...

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MAT1	102	10.0		0.495	6.0E-10
MATX62	102
	LAW	0.10	2.0	-0.010	-2.0

Field	Contents
MID	Material ID of the associated MAT1 (See comment 1). No default (Integer > 0)
MUMAX	Maximum viscosity. Default = 1030 (Real)
LAW	Indicates that material parameters MUi and ALFAi follow.
MUi	Parameter μi (Real)
ALFAi	Parameter αi (Real)
MAXWELL	Indicates that MAXWELL model parameter pairs GAMi and Ti follow.
GAMi	Stiffness ratio γi. (Real)
Ti	Time relaxation τi. (Real)

Comments

1.	The material identification number must be that of an existing MAT1 bulk data entry. Only one MATXi material extension can be associated with a particular MAT1.

2.	MATX62 is only applied in geometric nonlinear analysis subcases which are defined by ANALYSIS = EXPDYN. It is ignored for all other subcases.

3.	NU is defined on the corresponding MAT1.

4.	If no pair GAM1, T1 is given the law is hyper-elastic.

5.	The strain energy density W is computed using the following equation:

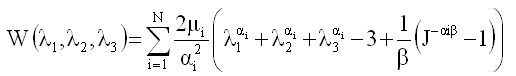
matx62_1

with λi being the ith principal stretch, J = λ1 * λ2 * λ3 being the relative volume and 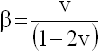matx62_2 . O < NU < 0.5

The ground shear modulus is:

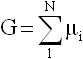
matx62_3

6.	This card is represented as a material in HyperMesh.