PAABSF

Bulk Data Entry

PAABSF – Frequency-Dependant Fluid Acoustic Absorber Property

Description

Defines the properties of the fluid acoustic absorber element.

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
PAABSF	PID	TZREID	TSIMID	S	A	B	K	RHOC

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
PAABSF	4	3	4	1.0	0.5

Field	Contents
PID	Property identification number. (Integer > 0)
TZREID	TABLEDi entry identification number that defines the resistance as a function of frequency. The real part of the impedance. (Integer > 0 or Blank)
TZIMID	TABLEDi entry identification number that defines the reactance as a function of frequency. The imaginary part of impedance. (Integer > 0 or Blank)
S	Impedance scale factor. Default = 1.0 (Real)
A	Area factor when 1 or 2 grid points are specified in the CAABSF entry. Default = 1.0 (Real > 0.0)
B	Equivalent damping coefficient. Default = 0.0 (Real)
K	Equivalent stiffness coefficient. Default = 0.0 (Real)
RHOC	Constant used in data recovery for calculating an absorption coefficient. RHO is the media density and C is the speed of sound in the media. Default = 1.0; current unused (Real)

Comments

1.	PAABSF is referenced by a CAABSF entry only.

If only one grid point is specified on the CAABSF entry, the impedance Z(f) = ZR + iZi is the total impedance at the point. If two grids are specified, then the impedance is the impedance per unit length. If three or four points are specified, then the impedance is the impedance per unit area. ZR(f) = TZREID(f) + B and Zi(f) = TZIMID(f) – K/(ω).

3.	The resistance represents a damper quantity B. The reactance represents a quantity of the type (ωM – K/ω). The impedance is defined as: Z = p/u where, p is the pressure and u is the velocity.

4.	The impedance scale factor S is used in computing element stiffness and damping terms as:

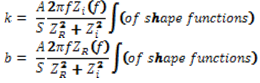
paabsf_eq

To create a non-reflecting boundary, set the values of the TABLEDi entry referenced by the TZREID field (Resistance-real part of Impedance) to be equal to

for all frequencies. This will allow the acoustic wave to propagate normally through the boundary, without reflection. This condition is called the Sommerfeld boundary condition.

Where, is the density of the fluid and, is the speed of sound in the fluid.

6.	This card is represented as a property in HyperMesh.