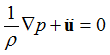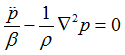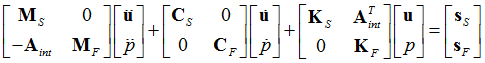Coupled frequency response analysis of fluid-structure models, commonly termed acoustic analysis, is generally performed to model sound propagation within a structural cavity, such as the interior of a vehicle or a musical instrument.
OptiStruct allows both direct and modal frequency response analysis for fluid-structure models. The responses of both the structural and fluid domains are computed; for the structural domain, these responses are the displacements and rotations of the structural grids, and for the fluid domain, these responses are the pressures at the fluid grid points.
The accelerations of structural grids at the fluid-structure interface excite the fluid domain and conversely, the pressures on the fluid grids at the fluid-structure interface excite the structural domain. Hence the problem is coupled and the motions of structural and fluid degrees-of-freedom are solved simultaneously.
Loading is sinusoidal with excitation frequency 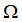 , and can be in the form of forces, acoustic sources enforced displacements, enforced velocities, and/or enforced accelerations. Frequency response loads and boundary conditions are defined in the bulk data section of the input deck. These are then referenced in a subcase definition through an SPC or DLOAD data selector.
, and can be in the form of forces, acoustic sources enforced displacements, enforced velocities, and/or enforced accelerations. Frequency response loads and boundary conditions are defined in the bulk data section of the input deck. These are then referenced in a subcase definition through an SPC or DLOAD data selector.
Damping may be defined for both the structural and fluid domains. For the structural domain damping may be defined through structural damping elements, material damping, structural damping (PARAM,G), or modal damping (SDAMPING referenced by a SDAMPING(STRUCT) subcase data selector). For the fluid domain damping may be defined through material damping, fluid damping (PARAM,GFL), or modal damping (SDAMPING referenced by a SDAMPING(FLUID) subcase data selector). In addition, the normalized admittance coefficient for porous materials can be specified by ALPHA on the MAT10 data.
Frequency dependent fluid acoustic absorber elements can be specified on the fluid faces of the fluid-structure boundary using the CAABSF elements. The absorber elements can be point, line, triangular, or quadrilateral in shape. The CAABSF data references the PAABSF data which is used to specify the frequency dependent resistance (real part of the impendence) and reactance (imaginary part of the impendence) as well as the area factors for point and line elements.
PARAM, LFREQFL and PARAM, HFREQFL can be used to exclude modes from a coupled modal frequency response analysis (Acoustic analysis).
Fluid-Structure Interface
The acoustic analysis is based on inviscid flow with linear pressure-density relation as:
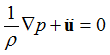
and the continuity equation is:
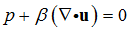
Where, p and u are the pressure of the fluid domain and displacement of the structural domain respectively, and 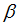 and
and 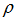 are the compressibility of the fluid domain and density of the structural domain, respectively.
are the compressibility of the fluid domain and density of the structural domain, respectively.
Combining the above equations, the governing equation of the fluid domain is:
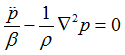
Effect of the structure on the fluid domain at the interface
After finite element discretization, the assembly of equations for the fluid domain is:
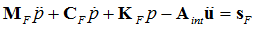
Where, MF, CF , KF , and sF are the mass matrix, damping matrix, stiffness matrix and source vector respectively, of the fluid domain.
The matrix Aint represents the interface matrix and 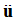 is the acceleration of the structural grids at the fluid-structure interface. (The pressure gradient at the interface will be influenced by the acceleration of the structural grids).
is the acceleration of the structural grids at the fluid-structure interface. (The pressure gradient at the interface will be influenced by the acceleration of the structural grids).
Effect of fluid on the structural domain at the interface
The structural equation assembly can be written as:
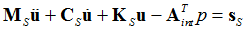
Where, MS, CS , KS , and sS are the mass matrix, damping matrix, stiffness matrix and source vector respectively, of the structural domain.
The matrix 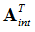 represents the transpose of the interface matrix and
represents the transpose of the interface matrix and 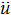 is the pressure at the interface fluid grids at the fluid-structure interface (The displacement, velocity and acceleration of the structural grids at the interface will be influenced by the pressure at the interface fluid grids).
is the pressure at the interface fluid grids at the fluid-structure interface (The displacement, velocity and acceleration of the structural grids at the interface will be influenced by the pressure at the interface fluid grids).
Coupled Fluid-Structure interface equation
Therefore the combined fluid-structure interface equation is:
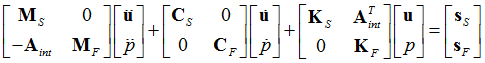
The above equations are solved simultaneously for unknowns in the structural and the fluid domains, either by direct frequency response or modal frequency response. For modal frequency response, OptiStruct will calculate the eigenspace for both structure and fluid domain automatically.
Loads on the Fluid Mesh
The fluid grid points can be loaded by specifying the load magnitude and GRID using the SLOAD data. The SLOAD data is referenced by the ACSRCE data which defines the dynamic characteristics of the load (DELAY, DPHASE, and a tabular listing of the load scale factor vs. frequency). In addition, the density and bulk modulus of the loaded fluid are specified on the ASRCE data. The material characteristics of the fluid must be specified in the ASRCE in case the same fluid GRID is shared by two different fluid meshes.
Fluid-Structure Interface Visualization and Refinement
OptiStruct has support for both grid-to-grid matching and non-matching interfaces. The interface is specified through the ACMODL card. If an ACMODL card is not specified in the input deck, the fluid-structure interface is automatically defined by OptiStruct based on default values for the ACMODL parameters.
Based on a search box specified on the ACMODL card, OptiStruct outputs an *.interface file, containing information about the fluid-structure interface. With the model loaded in HyperMesh, you can import the *.interface file to visualize the fluid-structure interface (ensure that the “FE overwrite” option is activated on import). The “^Fluid Faces at Interface” component is created, which allows you to view the interface found between the structural and fluid domains. If a component “^Acoustically Rigid Fluid Faces” is created, that means at those fluid surfaces, there are no structural grids found. A structural grid set “^Structural grids at Interface” is also created to display the structural grids found at the interface.
There are several steps you can take to improve the interface:
| 1. | Perform an OptiStruct check run. This will create the *.interface file, allowing you to visualize the interface. |
| 2. | If the interface is not as desired, you may create a new SET containing those fluid grids that describe the fluid boundary. |
| 3. | You can then specify the newly created set on the ACMODL card under FSET. |
| 4. | Perform another OptiStruct check run, and review the new interface. |
Using an External Fluid Structure Coupling Definition File
OptiStruct can use the binary ftn.70 coupling file generated by AKUSMOD instead of internally calculating the coupling. To use this option, add PARAM,AKUSMOD,YES to the input deck.
Modal and Panel Participation
Modal participation is a measure of how much each mode participates at a given frequency in a modal frequency response calculation. Output of modal participation may be requested for structural degrees of freedom as well as for fluid degrees of freedom. Calculation and output of modal participation can be requested, for any number of degrees of freedom, using the PFMODE I/O Option.
Panel participation is a measure of the influence of sets of specified structural grids, defined by PANEL bulk data entries. The response of a fluid grid is influenced through each panel or each grid at the acoustic interface. Calculation and output of the contribution from each panel at specific loading frequencies can be requested through the PFPANEL I/O Option, for modal frequency response. Also, the calculation and output of the contribution from each grid at the interface can be requested through the PFGRID I/O Option.
A file *.pfmode.pch is generated based on the definition of the I/O Options PFMODE and PFPANEL. The output for PFGRID would be in a H3D file. The results for PFMODE and PFPANEL are best plotted in HyperGraph, whereas the contour results for PFGRID are best visualized in HyperView.
Non-Reflecting Boundary
To create a non-reflecting boundary, set the values of the TABLEDi entry referenced by the TZREID field (Resistance-real part of Impedance) in the PAABSF data entry to be equal to 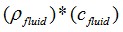 for all frequencies. This will allow the acoustic wave to propagate normally through the boundary, without reflection. This condition is called the Sommerfeld boundary condition.
for all frequencies. This will allow the acoustic wave to propagate normally through the boundary, without reflection. This condition is called the Sommerfeld boundary condition.
Where,  is the density of the fluid, and
is the density of the fluid, and  is the speed of sound in the fluid.
is the speed of sound in the fluid.
See Also:
Saving and Retrieving Normal Modes Analysis
AMLS (Automatic Multi-Level Sub-structuring) Eigensolver