|
»Click here to display Table of Contents«
|
Response Spectrum Analysis |
|
|
|
|
|
Response Spectrum Analysis |
|
|
|
|
Response Spectrum Analysis (RSA) is a technique used to estimate the maximum response of a structure for a transient event. Maximum displacement, stresses, and/or forces may be determined in this manner. The technique combines response spectra for a specified dynamic loading with results of a normal modes analysis. The time-history of the responses are not available.
Response spectra describes the maximum response versus natural frequency of a 1-DOF system for a specified dynamic loading. They are employed to calculate the maximum modal response for each structural mode. These modal maxima may then be combined using various methods, such as the Absolute Sum (ABS) method or the Complete Quadratic Combination (CQC) method, to obtain an estimate of the peak structural response.
RSA is a simple and computationally inexpensive method to provide an approximation of peak response, compared to conventional transient analysis. The major computational effort is to obtain a sufficient number of normal modes in order to represent the entire frequency range of input excitation and resulting response. Response spectra are usually provided by design specifications; given these, peak responses under various dynamic excitations can be quickly calculated. Therefore, it is widely used as a design tool in areas such as seismic analysis of buildings.
The equilibrium equation for a structure performing free vibration appears as the eigenvalue problem:
Where, K is the stiffness matrix of the structure and M is the mass matrix. Damping is neglected.
The solution of the eigenvalue problem yields n eigenvalues 
, where n is the number of degrees of freedom. The vector A is the eigenvector corresponding to the eigenvalue.
The eigenvalue problem is solved using the Lanczos or the AMSES method. Not all eigenvalues are required and only a small number of the lowest eigenvalues are normally calculated. The results of eigenvalue analysis are the fundamentals of response spectrum analysis.
Response spectrum analysis can be performed together with normal modes analysis in a single run, or eigenvalue analysis with Lanczos solver can be performed first to save eigenvalues and eigenvectors by using EIGVSAVE, which can be retrieved later by using EIGVRETRIEVE for response spectrum analysis.
It is assumed each individual mode behaves like a single degree-of-freedom system. The transient response at a degree of freedom is:
Where, A is the eigenvector, 
is modal participation factor, and 
is the response spectrum.
For loading due to base acceleration, the modal participation factor can be expressed as:
Where, A is the eigenvector, M is the mass matrix, and T is rigid body motion due to excitation.
In ABS modal combination, the peak response is estimated by:
In CQC modal combination, the peak response is estimated by:
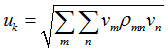
Where, 
is the modal response associated with mode m, and 
is the cross-modal coefficient.
The cross modal coefficient 
between modes m and n is calculated as:
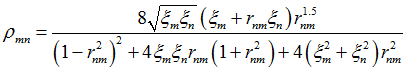
Where,
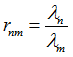is the ratio of eigenvalues of the modes
are the modal damping values of the two modes
In SRSS modal combination, the peak response is estimated by:
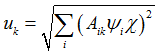
The SRSS method is less conservative than ABS method. It is more accurate when the modes are well separated.
The NRL method combines ABS and SRSS methods. It adds the maximum modal response by ABS method and the rest of the modes by SRSS method. The peak response is estimated by:
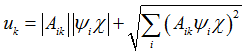
In order to estimate peak response due to dynamic excitations in different directions, the peak response in each direction must be combined to obtain total peak response. Methods such as ALG (algebraic) and SRSS (square root of sum of squares) can be used.
An RSA subcase may be explicitly identified by setting ANALYSIS=RSPEC, but it is also implicitly chosen for any subcase containing the RSPEC data selector (when the ANALYSIS entry is not present).
The following data selectors are recognized for an RSA subcase definition.
| • | METHOD – references an eigenvalue extraction bulk data definition (EIGRL). Only METHOD(STRUCTURE) is supported. This reference is required. |
| • | RSPEC – references an RSPEC bulk data entry where the combination rules, excitation DOF, and the input spectra are identified. This reference is required. |
| • | SDAMPING – references damping table bulk data entries (TABDMP1) to specify modal damping. This reference is required. |
| • | SPC – references single point constraint bulk data entries (SPCADD, SPC and SPC1). For RSA analysis, these entries define the base degrees of freedom where excitation is applied. |
Bulk data entries which have particular significance for RSA include:
| • | RSPEC – specifies combination rules, excitation DOF, and references the input spectra. |
| • | DTI,SPECSEL – defines response spectra. |
| • | EIGRL – defines parameters for eigenvalue extraction. |
| • | PARAM, LFREQ and PARAM, HFREQ – define the range of modes used in modal combinations. |
| • | TABDMP1 – specifies modal damping |
SUBCASE 100 RSPEC = 2 SPC = 5 SDAMPING = 12 METHOD = 24 $ BEGIN BULK $ PARAM, LFREQ, 0.1 PARAM, HFREQ, 1000. EIGRL, 24, 0.0, 1000. RSPEC, 2, ABS, CQC, 0.1 , 99, 2.0, 1.0, 0.0, 0.0 DTI, SPECSEL, 99, , A, 2, 0., 3, 0.02, , 4, 0.04, ENDREC TABDMP1, 12, … TABLED1, 2 +,… TABLED1, 3 +,… TABLED1, 4 +,… ENDDATA $ |
Results of interest from RSA include maximum displacement, stress and force. These are requested via the I/O Options DISPLACEMENT, STRESS and FORCE, respectively.
Saving and Retrieving Normal Modes Analysis
AMLS (Automatic Multi-Level Sub-structuring) Eigensolver
