HyperWorks Solvers

Example 47 - Concrete Validation

Example 47 - Concrete Validation

 Previous topic Next topic Expand/collapse all hidden text  

Example 47 - Concrete Validation

 Previous topic Next topic JavaScript is required for expanding text JavaScript is required for the print function  

ex47_concrete

Summary

RADIOSS includes the material model CONC to model concrete failure modeling under compression and tension.

Three kinds of tests are performed in this example:

•Uniaxial tests (uniaxial compression and uniaxial tension) where experimental results have been used to calibrate the model reference
•Multi-axial tests to evaluate the simulation/experiment correlation
•Cyclic tests to illustrate the right behavior of the model used

 

In order to simulate this experience, a model is created with the following details:

•A one element cube with eight node brick elements
•Concrete material law (/MAT/LAW24)

The simulation results are then compared to the experiment data.

 

Title

Concrete Validation

ex47_graph

Number

47.1

Brief Description

Three kinds of tests are performed in order to evaluate the simulation/experiment correlation and to illustrate the good behavior of the model used.

Keywords

•Concrete material law (/MAT/LAW24)
•Brick elements

RADIOSS Options

•Solid property (/PROP/SOLID)
•Boundary condition (/BCS)
•Imposed displacement (/IMPDISP)
•Imposed velocity (/IMPVEL)
•Pressure load (/PLOAD)

Input File

Concrete Failure: <install_directory>/demos/hwsolvers/radioss/47_concrete_test/*

Technical / Theoretical Level

Advanced

Overview

Physical Problem Description

The purpose of this example is to compare the simulation results to experimental data.

A concrete cube is subjected to various tests:

Kupfer Tests [2]

1.1: C000 - Uniaxial compressionprinciple stress symbol1 = -1; symbol2 = 0; symbol3 = 0
1.2: T000 - Uniaxial tensionprinciple stress symbol1 = 0; symbol2 = 0; symbol3 = 1
1.3: CC00 - Biaxial compressionprinciple stress symbol1 = -1; symbol2 = -1; symbol3 = 0
2.1: CC01 - Compression/Compressionprinciple stress symbol1 = 0.52; symbol2 = 0; symbol3 = -1
2.2: TC01 - Compression/Tensionprinciple stress symbol1 = -.052; symbol2 = 0; symbol3 = -1
2.3: TC02 - Compression/Tensionprinciple stress symbol1 = 0.102; symbol2 = 0; symbol3 = -1
2.4: TC03 - Compression/Tensionprinciple stress symbol1 = 0.204; symbol2 = 0; symbol3 = -1

 

Units: mm, ms, mg, MPa

The Concrete material law (/MAT/LAW24) has the following characteristics:

•Initial density = 0.0022 mg/mm3
•Concrete elasticity Young’s modulus Ec = 31700 MPa
•Poisson’s ratio ratio = 0.22
•Concrete uniaxial compression strength fc = 32.22 MPa
•Concrete biaxial strength fb/fc = 1.15
•Concrete confined strength f2/fc = 4.2
•Concrete confining stress so/fc = 0.8
•Concrete plasticity initial value of hardening parameter ky = 0.35
•Concrete plasticity dilatancy factor at yield αy = -0.6
•Concrete plasticity dilatancy factor at failure αf = -0.2
hmtoggle_plus1RADIOSS Card (Concrete)

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

/MAT/CONC/1

Concrete

#             RHO_I

              .0022                   0

#               E_c                  NU

              31700                 .22

#                fc            ft_on_fc            fb_on_fc            f2_on_fc            s0_on_fc

              32.22                   0                1.15                 4.2                  .8

#               H_t               D_sup             EPS_max

                  0                   0                   0

#               k_y                 r_t                 r_c                H_bp

                .35                   0                   0                   0

#           ALPHA_y             ALPHA_f               V_max

                -.6                  .2                   0

#               f_k                 f_0                H_v0

                  0                   0                   0

#                 E             sigma_y                 E_t

                  0                   0                   0

#            ALPHA1              ALPHA2              ALPHA3

                  0                   0                   0

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

 

Schickert and Winkler Tests

3.1: TRX1 - Meridian Compressionsymbolm = 51 MPa; symbol1 = 0.5; symbol2 = 0.5; symbol3 = -1
3.2: TRX0 - Meridian Shearsymbolm = 51 MPa; symbol1 = 1; symbol2 = 0; symbol3 = -1
3.3: TRX2 - Meridian Tensionsymbolm = 51 MPa; symbol1 = 2; symbol2 = -1; symbol3 = -1

 

Units: mm, ms, mg, MPa

The Concrete material law (/MAT/LAW24) has the following characteristics:

•Initial density = 0.0022 mg/mm3
•Concrete elasticity Young’s modulus Ec = 23000 MPa
•Poisson’s ratio ratio = 0.19
•Concrete uniaxial compression strength fc = 30.6 MPa
•Concrete data tensile tangent modulus Ht = -31700
•Concrete plasticity initial value of hardening parameter ky = 0.35
•Concrete plasticity base plastic modulus Hbp = 29170
•Concrete plasticity dilatancy factor at yield αy = -0.6
•Concrete plasticity dilatancy factor at failure αf = -0.2
hmtoggle_plus1RADIOSS Card (Concrete)

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

/MAT/CONC/1

Concrete

#             RHO_I

              .0022                   0

#               E_c                  NU

              23000                 .19

#                fc            ft_on_fc            fb_on_fc            f2_on_fc            s0_on_fc

               30.6                   0                   0                   0                   0

#               H_t               D_sup             EPS_max

             -31700                   0                   0

#               k_y                 r_t                 r_c                H_bp

                .35                   0                   0               29710

#           ALPHA_y             ALPHA_f               V_max

                -.6                  .2                   0

#               f_k                 f_0                H_v0

                  0                   0                   0

#                 E             sigma_y                 E_t

                  0                   0                   0

#            ALPHA1              ALPHA2              ALPHA3

                  0                   0                   0

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

 

Cyclic Tests

4.1: BBX0 Tension-Compression-Tension Cycle without Reinforcement

 

Units: mm, ms, mg, MPa

The Concrete material law (/MAT/LAW24) has the following characteristics:

•Initial density = 0.0022 mg/mm3
•Young modulus for concrete: Ec =57600 MPa
•Poisson’s ratio: ratio = 0.25
•Compressive strength of concrete: fc = 35.60 MPa
hmtoggle_plus1RADIOSS Card (Concrete)

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

/MAT/CONC/1

Concrete

#             RHO_I

              .0022                   0

#               E_c                  NU

              57600                 .25

#                fc            ft_on_fc            fb_on_fc            f2_on_fc            s0_on_fc

              35.60                   0                   0                   0                   0

#               H_t               D_sup             EPS_max

                  0                   0                   0

#               k_y                 r_t                 r_c                H_bp

                  0                   0                   0                   0

#           ALPHA_y             ALPHA_f               V_max

                  0                   0                   0

#               f_k                 f_0                H_v0

                  0                   0                   0

#                 E             sigma_y                 E_t

                  0                   0                   0

#            ALPHA1              ALPHA2              ALPHA3

                  0                   0                   0

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

 

4.2: BBX1 Tension-Compression-Tension Cycle with Reinforcement

The Concrete material law (/MAT/LAW24) has the following characteristics:

•Initial density = 0.0022 mg/mm3
•Young modulus for concrete: Ec =57600 MPa
•Poisson’s ratio: ratio = 0.25
•Compressive strength of concrete: fc = 35.60 MPa
•Reinforcement percentage: α3 = 1%
•Young modulus for steel: Ec = 210000 MPa
•Yield stress for steel: symboly = 500 MPa
hmtoggle_plus1RADIOSS Card (Concrete)

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

/MAT/CONC/1

Concrete

#             RHO_I

              .0022                   0

#               E_c                  NU

              57600                 .25

#                fc            ft_on_fc            fb_on_fc            f2_on_fc            s0_on_fc

               35.6                   0                   0                   0                   0

#               H_t               D_sup             EPS_max

                  0                   0                   0

#               k_y                 r_t                 r_c                H_bp

                  0                   0                   0                   0

#           ALPHA_y             ALPHA_f               V_max

                  0                   0                   0

#               f_k                 f_0                H_v0

                  0                   0                   0

#                 E             sigma_y                 E_t

             210000                 500                   0

#            ALPHA1              ALPHA2              ALPHA3

                  0                   0                 .01

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

The results for each test are:

•Stress in various directions as a function of deformations
•Von Mises stress as function of Pressure

 

Analysis, Assumptions and Modeling Description

Modeling Methodology

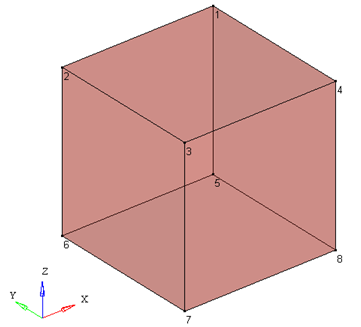
A 10 mm cube is modeled with a one element brick.

ex47_geometry

Fig 1: Geometry of the cube

RADIOSS Options Used

Boundary conditions depend on the test.

A scale factor of 0.1 (on time step for all elements) is used for “single elements models”.

Solid properties are:

•qa =1.1 and qb =0.05 (default values)
•Isolid = 1
•Iframe = 2 (co-rotational formulation)
•Istrain is set to 1 (to post-treat strains).
hmtoggle_plus1RADIOSS Card (Concrete)

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

/PROP/SOLID/1

Concrete

#  Isolid    Ismstr               Icpre               Inpts      Irot    Iframe                  dn

        1         0                   0                   0         0         2                   0

#               q_a                 q_b                   h

                1.1                0.05                   0

#            dt_min   Istrain

                  0         1

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----

 

Simulation Results and Conclusions

Curves

Test C000: Uniaxial Compression

The X displacement is fixed for nodes 2, 3, 6 and 7. A negative displacement is applied on the face defined by nodes 1, 4, 5 and 8.

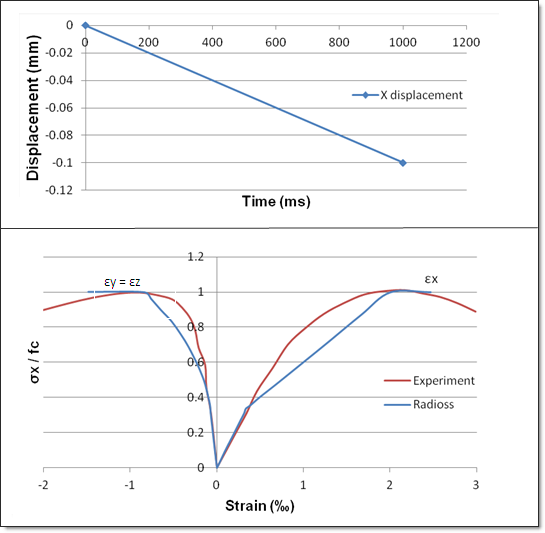
ex47_compression

Fig 2: Uniaxial compression with RADIOSS (blue curves) and experiment (red curves)

Comments

1.The stress/strain curve is made of three line segments.
2.After failure, the behavior obtained with RADIOSS curves (left) is perfectly plastic whereas there is experimentally a softening phenomenon (right).
3.The yield stress is obtained at σ = 0.337 fc for theoretical, numerical and experimental curves.

 

Test T000: Uniaxial Tension

The X displacement is fixed for nodes 2, 3, 6 and 7. A positive displacement is applied on the face defined by nodes 1, 4, 5 and 8.

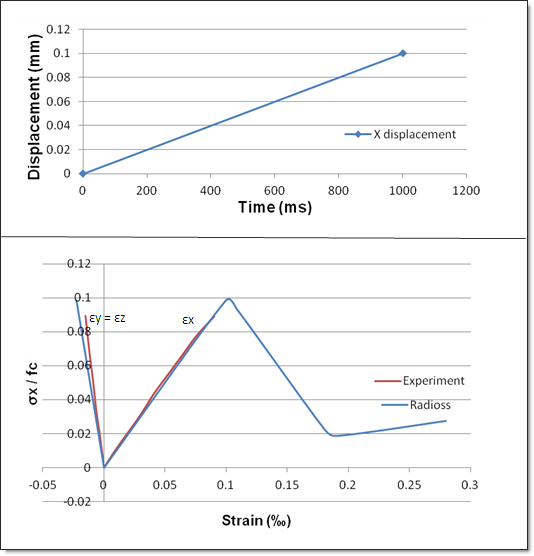
ex47_tension

Fig 3: Uniaxial Tension with RADIOSS (blue curves) and experiment (red curves)

Comments

1.Failure is modeled by stress and elastic modulus softening.
2.On the RADIOSS curve there is a residual stiffness in concrete after the softening: (1-Dsup)E
3.Dsup is set to 0.9 (default value = 0.99999).

 

Test CC00: Biaxial Compression

The X displacement is fixed on nodes 2, 3, 6 and 7. The Y displacement is fixed on nodes 3, 4, 7 and 8.

A displacement is applied in X direction on the face described by nodes 1, 4, 5 and 8 and in Y direction on the face described by nodes 1, 2, 5 and 6.

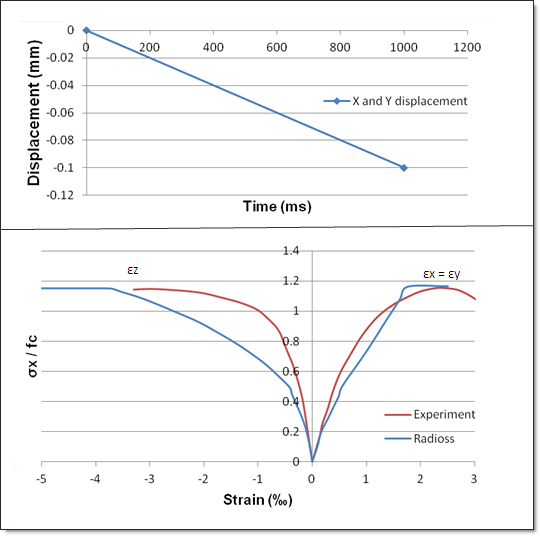
ex47_biaxial

Fig 4: Biaxial Compression with RADIOSS (blue curves) and experiment (red curves)

Comments

1.The yield stress is obtained at σ=0.197 fc for theoretical, numerical and experimental curves.
2.Failure mode is similar to uniaxial compression.

 

Test CC01 Compression/Compression

The X displacement is fixed on nodes 2, 3, 6 and 7. The Z displacement is fixed on nodes 5, 6, 7 and 8.

A pressure load is applied in X direction on the face described by nodes 1, 4, 5 and 8 and in Z direction on the face described by nodes 1, 2, 3 and 4.

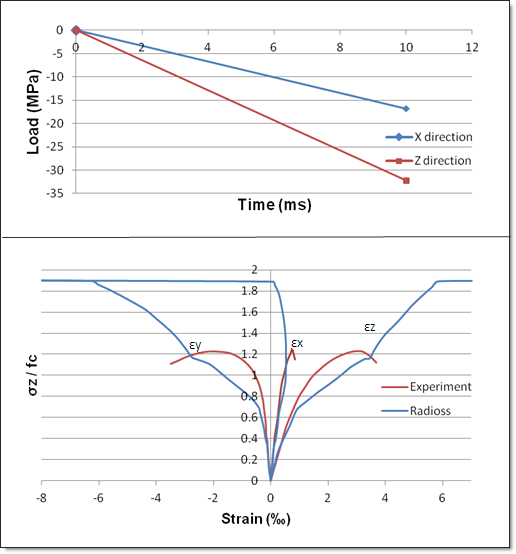
ex47_biaxial_2

Fig 5: Compression/Compression with RADIOSS (blue curves) and experiment (red curves)

Comments

1.Theoretical yield strength: 0.288 fc
2.Theoretical failure: 1.926 fc
3.Experimental failure: 1.22 fc
4.Theoretical and numerical results are the same, but different from experimental results; linear interpolation between the traction meridian and the compression meridian is too coarse for small confinement.

 

TC01 Compression/Tension

X displacement is fixed on nodes 2, 3, 6 and 7.

Z displacement is fixed on nodes 5, 6, 7 and 8.

A pressure load is applied in X direction on the face described by nodes 1, 4, 5 and 8, and in Z direction on the face described by nodes 1, 2, 3 and 4.

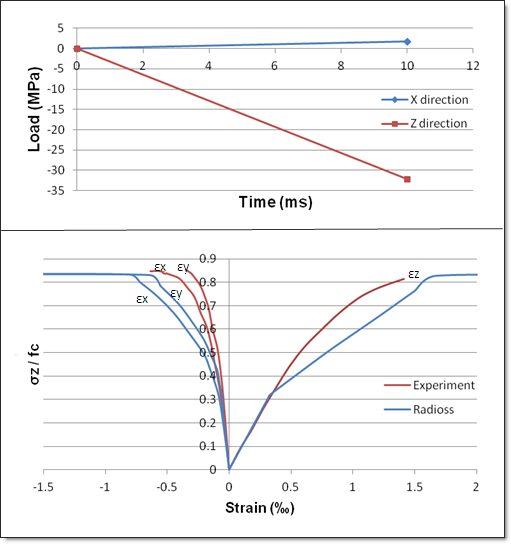
ex47_comp-tension

Fig 6: Compression/Tension with RADIOSS (blue curves) and experiment (red curves)

Comments

1.Theoretical yield strength: 0.327 fc
2.Theoretical failure: 0.83 fc
3.Experimental failure: 0.85 fc
4.Theoretical, numerical and experimental results are the same.

 

TC02 Compression/Tension

The X displacement is fixed on nodes 2, 3, 6 and 7. The Z displacement is fixed on nodes 5, 6, 7 and 8.

A pressure load is applied in X direction on the face described by nodes 1, 4, 5 and 8, and in Z direction on the face described by nodes 1, 2, 3 and 4.

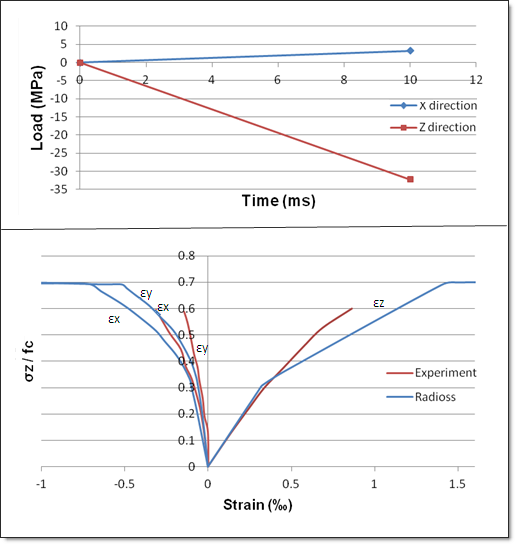
ex47_tc02

Fig 7: Compression/Tension with RADIOSS (blue curves) and experiment (red curves)

Comments

1.Theoretical yield strength: 0.3 fc
2.Theoretical failure: 0.7 fc
3.Experimental failure: 0.6 fc
4.Theoretical and numerical results are the same, but slightly different from experimental results.

 

TC03 Compression/Tension

The X displacement is fixed on nodes 2, 3, 6 and 7. The Z displacement is fixed on nodes 5, 6, 7 and 8.

A pressure load is applied in X direction on the face described by nodes 1, 4, 5 and 8, and in Z direction on the face described by nodes 1, 2, 3 and 4.

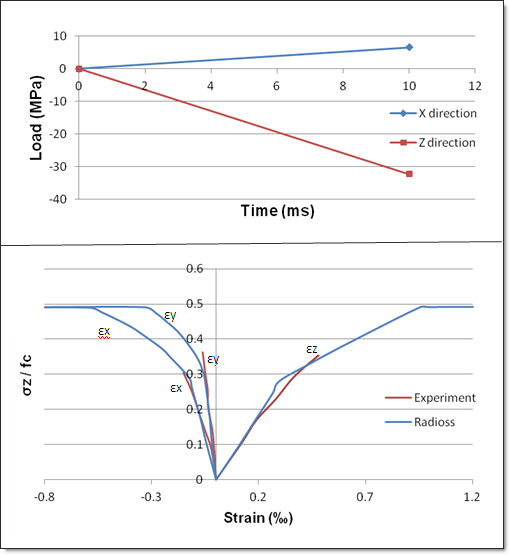
ex47_tc03

Fig 8: Compression/Tension with RADIOSS (blue curves) and experiment (red curves)

Comments

1.Theoretical yield strength: 0.28 fc
2.Theoretical failure: 0.5 fc
3.Experimental failure: 0.35 fc
4.Theoretical and numerical results are the same, but different from experimental results.

 

Test TRX00: Triaxial Meridian Shear

The X displacement is fixed on nodes 2, 3, 6 and 7. The Y displacement is fixed on nodes 3, 4, 7 and 8. The Z displacement is fixed on nodes 5, 6, 7 and 8.

A hydrostatic pressure of 51 MPa is applied on the sample.

A pressure load is applied in X direction on the face described by nodes 1, 4, 5 and 8, and in Z direction on the face described by nodes 1, 2, 3 and 4.

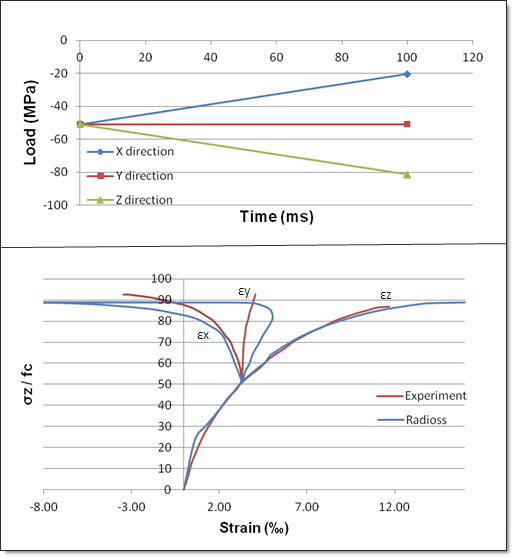
ex47_trx00

Fig 9: Triaxial Meridian Shear with RADIOSS (blue curves) and experiment (red curves)

Comments

1.Theoretical yield strength: 64.3 MPa
2.Theoretical failure: 88.9 MPa
3.Experimental failure: 93 MPa

 

Test TRX01: Triaxial Meridian Compression

The X displacement is fixed on nodes 2, 3, 6 and 7. The Y displacement is fixed on nodes 3, 4, 7 and 8. The Z displacement is fixed on nodes 5, 6, 7 and 8.

A hydrostatic pressure of 51 MPa is applied on the sample.

A pressure load is applied in X direction on the face described by nodes 1, 4, 5 and 8, in Y direction on the face described by nodes 1, 2, 5 and 6, and in Z direction on the face described by nodes 1, 2, 3 and 4.

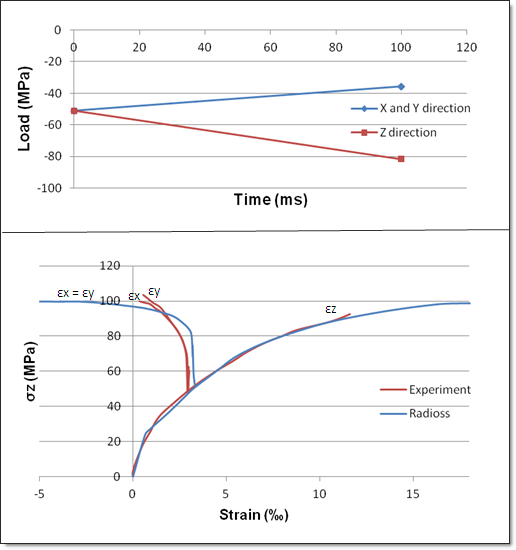
ex47_trx01

Fig 10: Triaxial Meridian Compression with RADIOSS (blue curves) and experiment (red curves)

Comments

1.Theoretical yield strength: 68.4 MPa
2.Theoretical failure: 99.7 MPa
3.Experimental failure: 103 MPa
4.The behavior of the model under hydrostatic loading is elastic, whereas there are non-linearities experimentally.

 

Test TRX02: Triaxial Meridian Compression

The X displacement is fixed on nodes 2, 3, 6 and 7. The Y displacement is fixed on nodes 3, 4, 7 and 8. The Z displacement is fixed on nodes 5, 6, 7 and 8.

An hydrostatic pressure of 51 MPa is applied on the sample.

A pressure load is applied in X direction on the face described by nodes 1, 4, 5 and 8, in Y direction on the face described by nodes 1, 2, 5 and 6, and in Z direction on the face described by nodes 1, 2, 3 and 4.

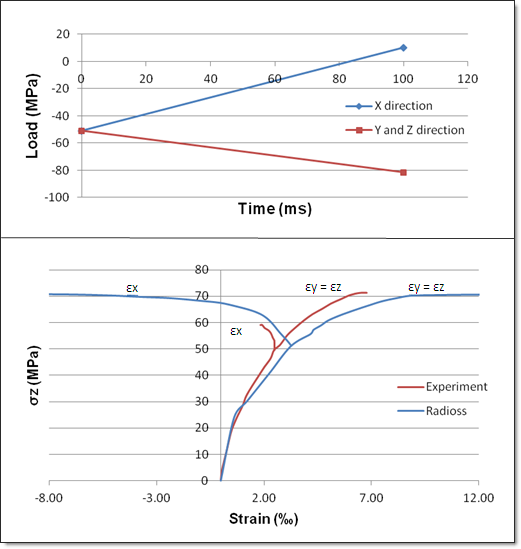
ex47_trx02

Fig 11: Triaxial Meridian Compression with RADIOSS (blue curves) and experiment (red curves)

Comments

1.Theoretical yield strength: 57.9 MPa
2.Theoretical failure: 70.8 MPa
3.Experimental failure: 72 MPa

 

Test BBX0: Tension-Compression-Tension Cycle without Reinforcement

A displacement is applied in the Z direction on the face defined by nodes 1, 2, 3 and 4 with a tension-compression-tension cycle as shown below:

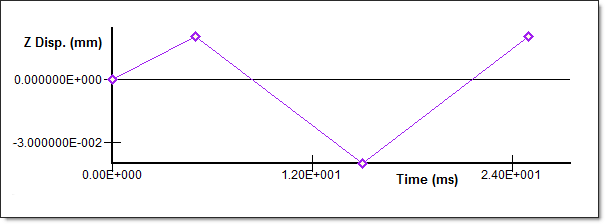
ex47_bbx0

Fig 12: Velocity imposed

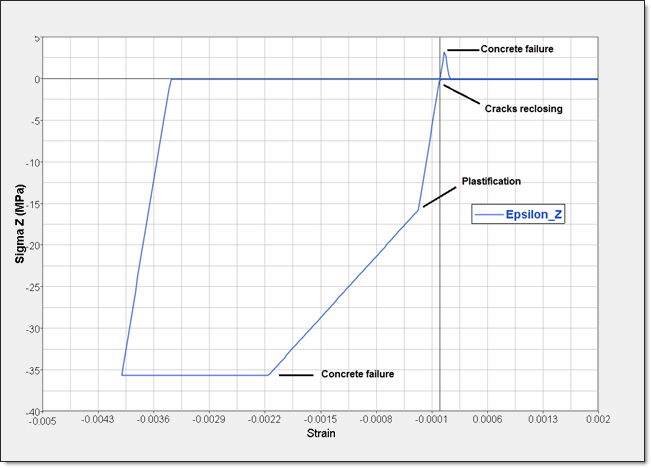
ex47_bbx0A

Fig 13: Cycle without reinforcement

This test illustrates the behavior of the model LAW24:

•Failure, damage and cracks reopening
•Cracks reclosing
•Plastification and hardening
•Compressive strength
•Residual plastic deformation

 

Test BBX1: Tension-Compression-Tension Cycle with Reinforcement

A velocity is set among the Z direction on the face defined by nodes 1, 2, 3 and 4 with a tension-compression-tension cycle, as shown below:

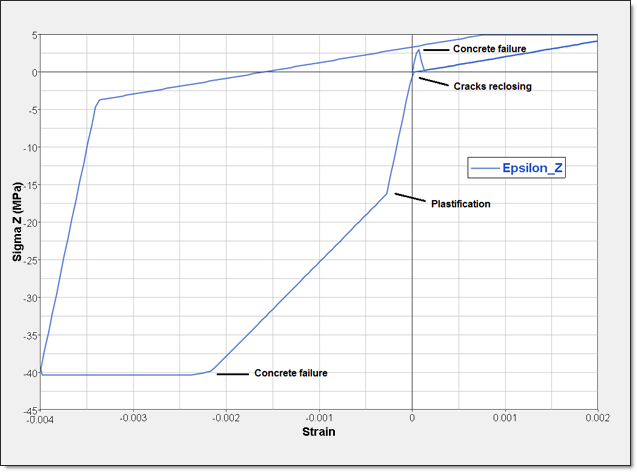
ex47_bbx1

Fig 14: Cycle with reinforcement

Comments

1.Steel reinforcement improves compressive and tensile strength by 5 MPa compared to the same model without steel reinforcement.

 

Von Mises / Pressure Curves

The following von Mises/Pressure curves show the different areas described by tensile and compressive tests.

Each orange point corresponds to the failure point of the model considered.

fc is the uniaxial compressive strength.

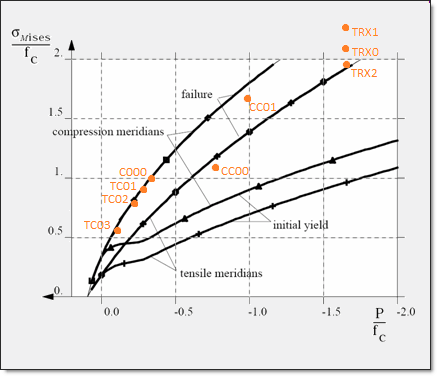
ex47_vonmises

Fig 15: von Mises/Pressure curves

Conclusion

Under complex loading, concrete mechanic behavior between RADIOSS simulation, theory and experiments are demonstrated. With three kinds of tests, the mechanic behavior of concrete can be well characterized using LAW24.

References

[1] A non-uniform hardening plasticity model for concrete materials, Mechanics of Materials, D.J. Han and W.F. Chen, 1984.

[2] Behavior of Concrete under Biaxial Stresses, Journal of the Engineering Mechanics Division, ASCE, V. 99, No. 4, pp. 853-866u, LKupfer, B., and Gerstle, K., 1973.