Example 52 - Creep and Stress Relaxation |

|

|

|

|
|
Example 52 - Creep and Stress Relaxation |

|

|

|

|
The aim of this example is to introduce how to use typical visco-elastic material to simulate creep and stress relaxation tests. Stress relaxation is the phenomena of how polymers relieve stress under constant strain, and creep is the phenomena of how polymers or metal move slowly or deform permanently under constant stresses. This simulates the creep and relaxation processes over a short period of time in quasi-static.
TitleCreep and Stress Relaxation |
|
||||||||
Number52 |
|||||||||
Brief DescriptionUse visco-elastic material law /MAT/LAW40 to simulate the creep and stress relaxation. |
|||||||||
Keywords |
|||||||||
RADIOSS Options
|
|||||||||
Input fileCreep and Stress Relaxation: <install_directory>/demos/hwsolvers/radioss/52_creep_and_stress_relaxation/* |
|||||||||
Technical / Theoretical LevelAdvanced |
|||||||||
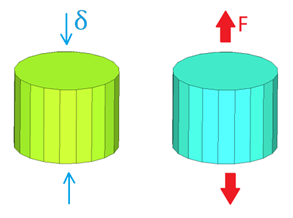
A foam sample with dimension: Radius 10 mm and high 15 mm.
| • | For stress relaxation test: The foam sample has been compressed until a given strain and kept in this state. |
| • | For creep test: The foam sample has been tensile under constant force. |

Fig 1: Problem description
Units: mm, s, Mg, N, MPa
To describe the phenomenon stress relaxation and creep, use viscous material law /MAT/LAW40 with the following characteristics of foam:
| • | Initial density = 2e-9 [Mg/mm3] |
| • | Bulk modulus = 66.67 [MPa] |
| • | Long time shear modulus Ginf = 10 [MPa] |
| • | Shear modulus G1 = 90 [MPa] |
| • | Decay constant |
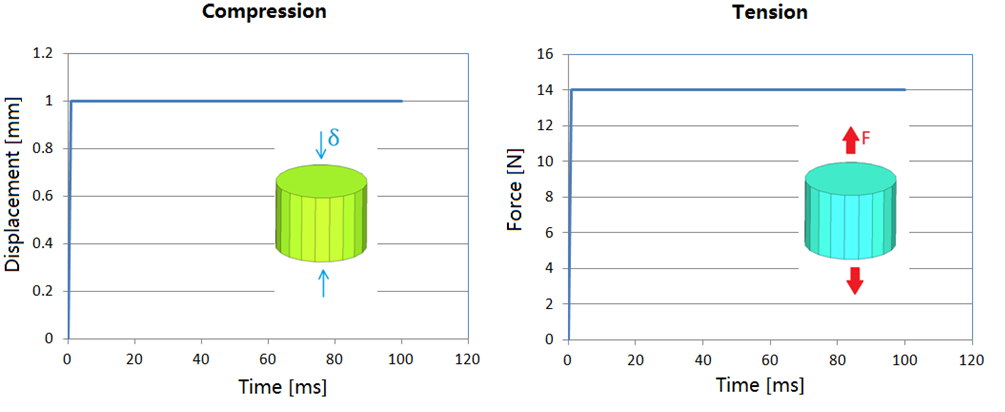
Fig 2: Stress relaxation test under constant displacement and creep test under constant force
For stress relaxation test: The foam sample has been compressed under constant displacement (/IMPDISP).
For creep test: The foam sample has been tensile under constant force (/CLOAD).
The stress relaxation test shows stress relieve under constant displacement with different relaxation parameters (Decay constant, ![]() defined as the inverse of relaxation time
defined as the inverse of relaxation time ![]() ) and
) and ![]() shows a different stress relive tendency.
shows a different stress relive tendency.
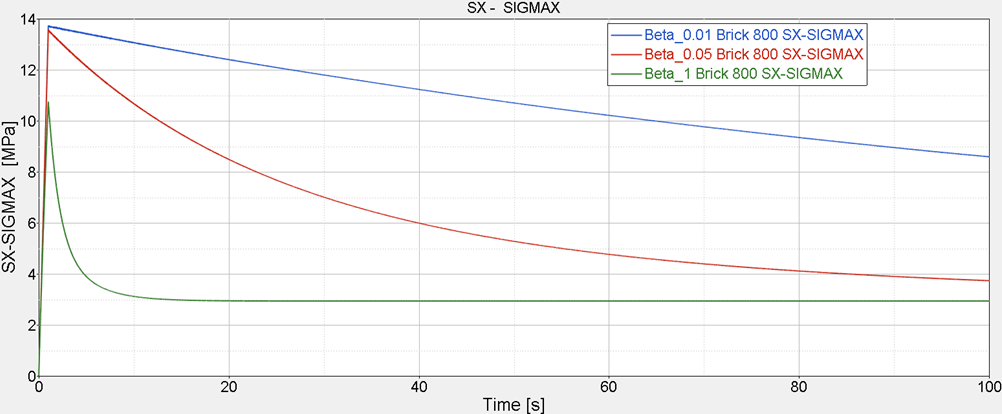
Fig. 3: Stress relieved with different Decay constant β in stress relaxation test under constant displacement
The creep test shows deformation increased under constant force and with different relaxation parameter ![]() it shows a different deformation increase tendency.
it shows a different deformation increase tendency.
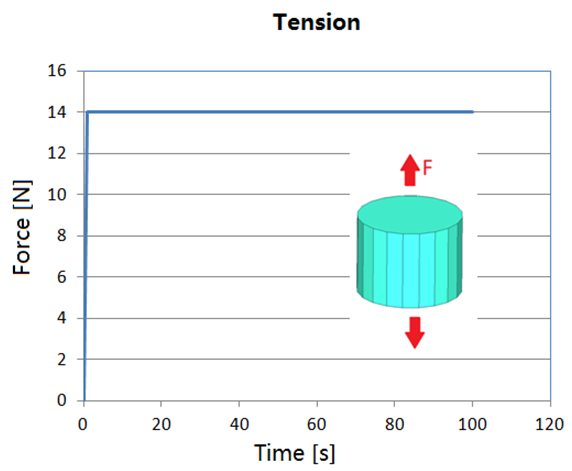
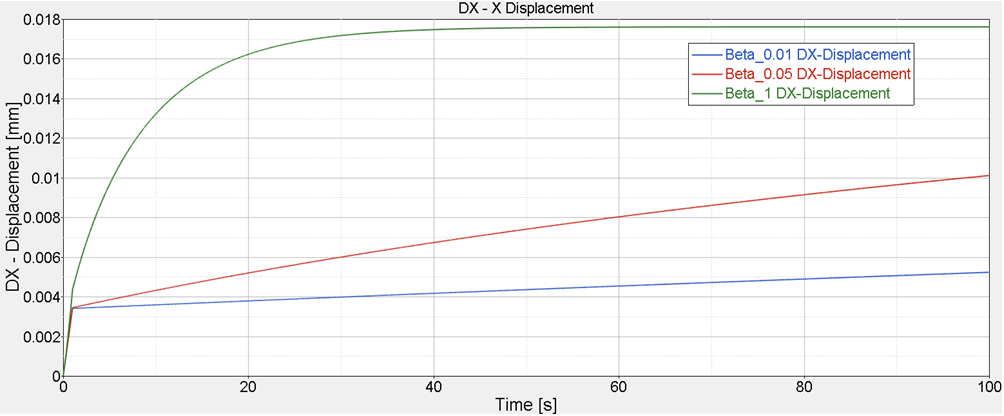
Fig. 4: Sample deformed with Decay constant β in creep test under constant force
In LAW40 shear modulus is reduced with time and tends to G∞ after an infinite period of time. The softening speed is determined by relaxation parameter ![]() . Higher relaxation parameter means quick softening.
. Higher relaxation parameter means quick softening.

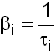 with
with ![]()
The general case of viscous materials represents time-dependent in elastic behavior. Creep is time-depended deformation and stress relaxation is a time-depended decrease in stress. Viscous material can describe these two phenomenons. In RADIOSS, the following material laws describe viscous:
| • | /MAT/LAW34: visco-elastic generalized Maxwell model, Boltzmann (solids) |
| • | /MAT/LAW35: visco-elastic generalized Maxwell-Kelvin-Voigt (shells + solids) |
| • | /MAT/LAW38: visco-elastic tabulated (solids) |
| • | /MAT/LAW40: visco-elastic generalized Maxwell-Kelvin (solids) |
| • | /MAT/LAW42: Ogden/Mooney-Rivlin with Prony viscosity (Hyperelastic materials) |
| • | /MAT/LAW62: Ogden (Hyperelastic materials) |
| • | /MAT/LAW70: visco-elastic tabulated (solids) |
| • | /MAT/LAW77: visco-elastic tabulated with porosity and air flow |
| • | /MAT/LAW33: visco-elastic plastic (solids) and user-defined yield function |
| • | /MAT/LAW52: Gurson, visco-elasto-plastic porous metals, and strain rate dependent |
| • | /MAT/LAW66: semi-analytical plastic model. Yield surface built from curves in tension, compression and shear + /VISC/PRONY |
The creep compliance and the relaxation modulus are often modeled by combinations of springs and dashpots. The two typical simple schematic model of visco-elastic material are Maxwell model and Kelvin-Voigt model. The Maxwell model represents the material relaxation, but it is only accurate for secondary creep (creep with slow decrease in creep strain rate) as the viscous strains after unloading are not taken into account. The plasticity can be introduced in the models by using a plastic spring. Base on the Maxwell and Kelvin-Voigt models adding other springs could get a generalized model. The Maxwell and Kelvin-Voigt models are appropriate for ideal stress relaxation and creep behaviors. Although, they are not adequate for most of physical materials. A generalization of these laws, like LAW34, LAW35 and LAW40 are a better choice, which can describe deviatory behavior of material.
Maxwell model |
Kelvin-Voigt model |
|---|---|
|
|