Block Format Keyword
/MAT/LAW73 - Thermal Hill Orthotropic Material
Description
This law describes the Thermal Hill orthotropic material and is applicable only to shell elements. This law differs from /MAT/LAW43 (HILL_TAB) by the fact that yield stress not only depends on strain rate and plastic strain, but also on temperature (it is defined by a user table).
Format
(1)
|
(2)
|
(3)
|
(4)
|
(5)
|
(6)
|
(7)
|
(8)
|
(9)
|
(10)
|
/MAT/LAW73/mat_ID/unit_ID
|
mat_title
|
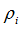
|
|
|
|
|
|
|
|
|
E
|
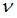
|
|
|
|
|
|
|
fct_IDE
|
|
Einf
|
CE
|
Blank
|
r00
|
r45
|
r90
|
Chard
|
Iyield0
|
|
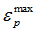
|
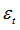
|
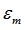
|
|
|
|
|
Tab_ID
|
|
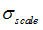
|
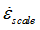
|
|
|
|
|
Ti
|
Cp
|
|
|
|
|
|
|
|
Field
|
Contents
|
SI Unit Example
|
mat_ID
|
Material identifier
(Integer, maximum 10 digits)
|
|
unit_ID
|
Optional unit identifier
(Integer, maximum 10 digits)
|
|
mat_title
|
Material title
(Character, maximum 100 characters)
|
|
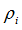
|
Initial density
(Real)
|
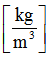
|
E
|
Initial Young’s modulus
(Real)
|
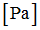
|
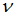
|
Poisson’s ratio
(Real)
|
|
fct_IDE
|
Function identifier for the scale factor of Young modulus, when Young modulus is function of the plastic strain.
Default = 0 in this case the evolution of Young depends on Einf and CE.
(Integer)
|
|
Einf
|
Saturated Young’s modulus for infinitive plastic strain
(Real)
|
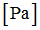
|
CE
|
Parameter for Young’s modulus evolution
(Real)
|
|
r00
|
Lankford parameter 0 degree (Comment 3)
Default = 1.0 (Real)
|
|
r45
|
Lankford parameter 45 degrees
Default = 1.0 (Real)
|
|
r90
|
Lankford parameter 90 degrees
Default = 1.0 (Real)
|
|
Chard
|
Hardening coefficient
(Real)
= 0: hardening is full isotropic model
= 1: hardening uses the kinematic Prager-Ziegler model
= between 0 and 1: hardening is interpolated between the two models
|
|
Iyield0
|
Yield stress flag
(Integer)
= 0: average yield stress input
= 1: yield stress in orthotropic direction 1
|
|
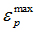
|
Failure plastic strain
Default = 1.0 x 1030 (Real)
|
|
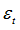
|
Tensile failure strain at which stress starts to reduce
Default = 1.0 x 1030 (Real)
|
|
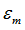
|
Maximum tensile failure strain at which the stress in element is set to zero
Default = 2.0 x 1030 (Real)
|
|
Tab_ID
|
Table identifier for yield stress definition
(Integer)
|
|
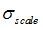
|
Yield stress scale factor
Default set to 1.0 (Real)
|
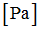
|
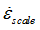
|
Strain rate scale factor
Default set to 1.0 (Real)
|
|
Ti
|
Initial temperature
Default set to 293 K (Real)
|
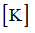
|
Cp
|
Specific heat per mass unit
(Real)
|

|
|
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
g mm ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW73/1/1
steel
# RHO_I
0.0078
# E NU
210000.0 0.3
# fct_IDE E_inf CE
0 0 0
# R00 R45 R90 C_hard I_yield0
1.6 1.6 1.6 0.0 0
# EPSP_MAX EPS_T1 EPS_T2
0 0 0
# table_ID SIGMA_SCALE EPSPT_SCALE
10 0 0
# TI CP
273. 4.
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/TABLE/1/10
table
3
1011 0.0 273.
1013 0.02 300.
1013 0.04 300.
1012 0.0 300.
1012 0.02 273.
1012 0.04 273.
/FUNCT/1011
1st
0.0 185.0
0.1 339.0
1.0 339.0
/FUNCT/1012
2nd
0.0 190.0
0.1 344.0
1.0 344.0
/FUNCT/1013
3rd
0.0 195.0
0.1 349.0
1.0 349.0
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
|
| 2. | The yield stress is defined by a user function and the yield stress is compared to equivalent stress: |
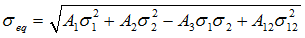
| 3. | Angles for Lankford parameters are defined with respect to orthotropic direction 1. |
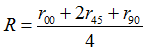 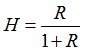
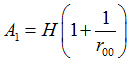 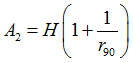
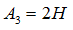 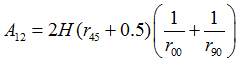
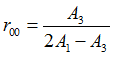 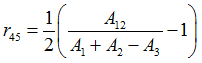
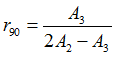
The Lankford parameters 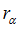 is the ratio of plastic strain in plane and plastic strain in thickness direction is the ratio of plastic strain in plane and plastic strain in thickness direction 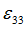 . .
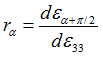
Where,  is the angle to the orthotropic direction 1. is the angle to the orthotropic direction 1.
This Lankford parameters  could be determined from a simple tensile test at an angle could be determined from a simple tensile test at an angle  . .
A higher value of R means better formability.
| 4. | If 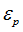 (plastic strain) reaches (plastic strain) reaches 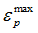 , in one integration point, the corresponding shell element is deleted. , in one integration point, the corresponding shell element is deleted. |
| 5. | If 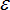 1 (largest principal strain) 1 (largest principal strain) 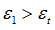 , stress is reduced using the following relation: , stress is reduced using the following relation: |
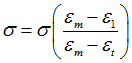
| 6. | If 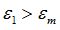 , the stress is reduced to 0 (but the element is not deleted). , the stress is reduced to 0 (but the element is not deleted). |
| 7. | This law always uses iterative projection for plasticity (Iplas from the property set is ignored). |
| 8. | This law is not available with global formulation for plasticity (N= 0 in the property shell is not available). |
| 9. | The table for yield stress definition must be a 3-dimensional table whose parameters respectively represent plastic strain, strain rate, and temperature 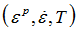 . Values of the table are yield stress values. . Values of the table are yield stress values. |
| 10. | If 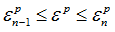 and and 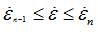 and and 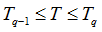 yield is linearly interpolated between the eight values of the table corresponding to yield is linearly interpolated between the eight values of the table corresponding to 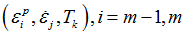 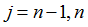 , , 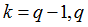 . . |
| 11. | If 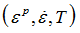 falls out of the range of the table, yield stress is obtained by linear extrapolation. Thus it is necessary to input into the table the static curves corresponding to zero strain rate (entry falls out of the range of the table, yield stress is obtained by linear extrapolation. Thus it is necessary to input into the table the static curves corresponding to zero strain rate (entry 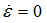 should belong to the table definition). should belong to the table definition). |
If the /HEAT/MAT option is not associated to the material identifier, adiabatic conditions are assumed and temperature is computed as:
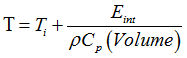
where,
Eint is the internal energy computed by RADIOSS,
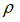 and Volume are the current density, and volume, and Volume are the current density, and volume,
Cp is the heat capacity per mass unit.
Otherwise, the finite element formulation for heat transfer must be asked for (Iform = 1 in option /HEAT/MAT); initial temperature and specific heat input in the option /HEAT/MAT will then be used.
| 12. | If the yield stresses have been obtained in the orthotropic direction 1, define Iyield0 = 1; otherwise Iyield0 = 0. |
|
See Also:
Material Compatibility
Law Compatibility with Failure Model
/MAT/LAW2 and /MAT/LAW36 in User's Guide
Hill's Law for Orthotropic Plastic Shells in Theory Manual







