MATX21

Bulk Data Entry

MATX21 – Material Property Extension for Rock-Concrete Material for Geometric Nonlinear Analysis

Description

Defines additional material properties for Rock-Concrete material for geometric nonlinear analysis. This law is based on the Drücker-Prager yield criteria and is used to model materials with internal friction such as rock-concrete. The plastic behavior of these materials is dependent on the pressure in the material. This law is only applicable to solid elements.

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MATX21	MID	A0	A1	A2	AMAX
	TPID	KT	FSCAL	PMIN	B	MUMAX	PEXT

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MAT1	102	3.1E10		0.33	1000.0
MATX21	102			3
	1	1E10

Field	Contents
MID	Material ID of the associated MAT1. See comment 1. No default (Integer > 0)
A0	Coefficient. (Real)
A1	Coefficient. (Real)
A2	Coefficient. (Real)
AMAX	Von Mises limit. Default = 1030 (Real > 0)
TPID	Identification number of a TABLES1 that defines the volumetric strain vs. pressure function. No default (Integer > 0)
KT	Tensile bulk modulus. (Real > 0.0)
FSCAL	Scale factor for pressure function. Default = 1.0 (Real)
PMIN	Minimum pressure. Default = -1030 (Real)
B	Unloading bulk modulus. (Real > 0.0)
MUMAX	Maximum compression volumetric strain. (Real)
PEXT	External pressure. Is required if relative pressure formulation is used. In this specific case, yield criteria and energy integration require the value of total pressure. Default = 0.0 (Real)

Comments

1.	The material identification number must be that of an existing MAT1 bulk data entry. Only one MATX21 material extension can be associated with a particular MAT1.

2.	MATX21 is only applied in geometric nonlinear analysis subcases which are defined by ANALYSIS = EXPDYN. It is ignored for all other subcases.

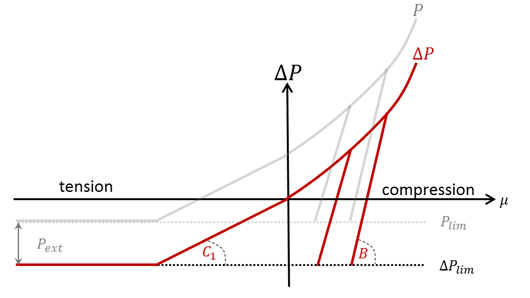
3.	Hydrodynamic behavior is given by a user-defined function P = f(µ)

where, P is the pressure in the material, and µ is the volumetric strain.

matx21_1

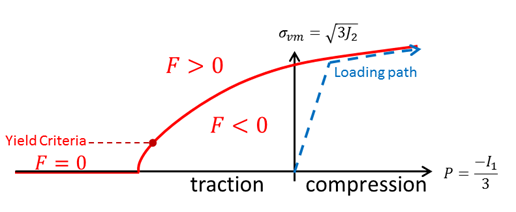
4.	Drücker-Prager yield criteria uses a modified von Mises yield criteria to incorporate the effects of pressure for massive structures:

F = J2 - (A0 + A1P + A2P2)

Where,

J2 is the second invariant of deviatoric stress.

P is the pressure.

A0, A1, and A2 are material coefficients.

A1 = A2 = 0 means that the yield criteria is von Mises ()

matx21_2

5.	It is recommended to set unloading bulk modulus, B equal to the initial slope of function describing P(µ) and tensile bulk modulus KT equal to 1/100 of unloading bulk modulus. B and KT must be positive.

1.	This card is represented as an extension to a MAT1 material in HyperMesh.