MATX33

Bulk Data Entry

MATX33 – Material Property Extension for Visco-Elastic Plastic Foam Material for Geometric Nonlinear Analysis

Description

Defines additional material properties for visco-elastic plastic foam material for geometric nonlinear analysis.

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MATX33	MID	KA	TID	FSCALE	P0	PHI	EPSV0
	A	B	C	E1	E2	ET	ETAC	ETAS

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MAT1	133	0.11		0.11	9.92E-07
MATX33	133	0

Field	Contents
MID	Material ID of the associated MAT1. See comment 1. No default (Integer > 0)
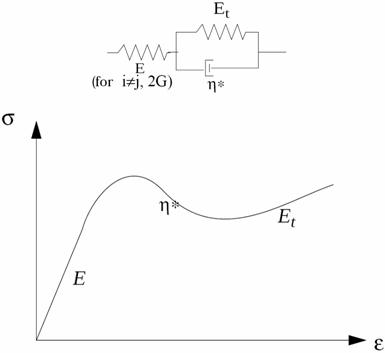
KA	Analysis type flag. Default = ELAST (Character = ELAST or VISCO) ELAST: skeletal behavior before yield is elastic. VISCO: skeletal behavior before yield is visco-elastic.
TID	Identification number of TABLES1 entry that defines the yield stress vs. volumetric strain curve. If defined, σy vs. is read from input of the curve. No default (Integer > 0)
FSCALE	Scale factor for stress in yield curve. Default = 1.0 (Real)
P0	Initial air pressure. See comment 4. Default = 0.0 (Real)
PHI	Ratio of foam to polymer density. Default = 0.0 (Real)
EPSV0	Initial volumetric strain. Default = 0.0 (Real)
A	Yield parameter. Default = 0.0 (Real)
B	Yield parameter. Default = 1.0 (Real)
C	Yield parameter. Default = 1.0 (Real)
E1	Coefficient for Young's modulus update. No default (Real)
E2	Coefficient for Young's modulus update. No default (Real)
ET	Tangent modulus. No default (Real > 0)
ETAC	Viscosity coefficient in pure compression. Default = 1.0 (Real > 0)
ETAS	Viscosity coefficient in pure shear. Default = 1.0 (Real > 0)

Comments

1.	The material identification number must be that of an existing MAT1 bulk data entry. Only one MATXi material extension can be associated with a particular MAT1.

2.	MATX33 is only applied in geometric nonlinear analysis subcases which are defined by ANALYSIS = EXPDYN. It is ignored for all other subcases.

3.	This material can be used only with solid elements, typically used to model low density, closed cell polyurethane foams such as impact limiters.

4.	The air pressure is computed as:

Pair = P0 * / (1+ - Φ), with = 0 + V/V0 - 1

where, is the volumetric strain, Φ is the porosity, P0 is the initial air pressure, 0 is the initial volumetric strain. The volumetric strain < 0 in compression.

5.	If TID is blank or zero, then

σy = A + B(1+ Cγ), with = V/V0 - 1 = ρ/ρ0 - 1 = -μ/(1+μ)

6.	The Young’s modulus used in the calculation is:

E = max(E, E1 + E2)

matx33

This material assumes NU = 0 no matter what is defined on the corresponding MAT1. Hence, G = 0.5 * E.

7.	This card is represented as an extension to a MAT1 material in HyperMesh.