MATX38

Bulk Data Entry

MATX38 – Material Property Extension for Viscoelastic Foam Tabulated Material (Tabulated form) for Geometric Nonlinear Analysis

Description

Defines additional material properties for viscoelastic foam tabulated material (tabulated form) for geometric nonlinear analysis.

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MATX36	MID	E0	NUT	NUC	RNU	IFLAG	ITOTA
	BETA	H	RD	KR	KD	THETA
	KAIR	NP	FSCALEP
	P0	RP	PMAX	PHI
	TIDUN		FSCAUN	EPSUN	A	B
			CUTOFF	IINSTA
	EFINAL	EPSFIN	LAMBDA	VISC	TOL
	TIDL1	TIDU1	FSCA1	EPSR1
	...	...	...
	TIDLi	TIDUi	FSCAi	EPSRi

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MAT1	102	60.4		0.33	2.70E-06
MATX38	102
	1.0-30	1.0	0.5			0.67
			1.0




	4		1.0	0.0

Field	Contents
MID	Material identifier of the associated MAT1 Bulk Data Entry. See comment 1. No default (Integer > 0)
E0	Minimum tension modulus, used for interface and time step computation No default (Real > 0)
NUT	Maximum Poisson's Ratio in tension Default = 10-30 (Real > 0)
NUC	Maximum Poisson's Ratio in compression No default (Real > 0)
RNU	Exponent for Poisson's ratio computation No default (Real > 0)
IFLAG	Analysis formulation type flag Default = 0 (Integer = 0 or 1) = 0: corresponds to the viscoelastic foam tabulated material - visco-elasticity is computed in each principal stress direction = 1: behavior is linear in both tension and compression, following Hook's relations (see Comment 7)
ITOTA	Incremental formulation flag Default = 0 (Integer = 0, 1, 2 or 3) Total: 0 or 1 = 0: behavior in tension is linear = 1: behavior in tension is read from stress curves Incremental: 2 or 3 = 2: behavior in tension is linear = 3: behavior in tension is read from stress curves
BETA	Relaxation rate for unloading Default = 10-30 (Real)
H	Hysteresis coefficient for unloading Default = 1.0 (Real)
RD	Damping factor on strain rate Default = 0.5 (Real)
KR	Recovery model flag on unloading for hysteresis Default = 0 (Integer) = 0: No stress recovery on unloading = 1: Stress recovery on unloading
KD	Decay model flag, hysteresis type Default = 0 (Integer = 0, 1 or 2) = 0: Decay is active during loading and unloading = 1: Decay is active only during loading = 2: Decay is active only during unloading
THETA	Integration coefficient for instantaneous module update Default = 0.67 (Real)
KAIR	Air content computation flag Default = 0 (Integer = 0, 1 or 2) = 0: No confined air content = 1: Confined air content computation active (see Comment 9) = 2: Read hydrostatic curve (number defined by NP). The difference between pure compression and hydrostatic will be taken into account.
NP	Pressure curve number (pressure vs. relative volume) No default (Integer)
FSCALEP	Pressure curve scale factor No default (Real)
P0	Atmospheric pressure No default (Real)
RP	Relaxation rate of pressure Default = 10-30 (Real > 0)
PMAX	Maximum air pressure Default = 1030 (Real > 0)
PHI	Porosity (density of foam/density of polymer) No default (Real)
TIDUN	Identification number of a TABLES1 that defines the unloading yield stress vs. plastic strain curve "i" corresponding to EPSRUN. No default (Integer > 0)
FSCAUN	Unloading function scale factor Default = 1.0 (Real)
EPSUN	Unloading strain rate (must be greater than EPSR1) (Real)
A	Exponent for stress interpolation Default = 1.0 (Real)
B	Exponent for stress interpolation Default = 1.0 (Real)
CUTOFF	Tension cutoff stress Default = 1030 (Real > 0)
IINSTA	Material instability control flag Default = 0 (Integer) = 0: No material instability control = 1: Material instability control
EFINAL	Maximum tension modulus Default = E0 (Real)
EPSFIN	Absolute value of strain at final modulus Default = 1.0 (Real)
LAMBDA	Modulus interpolation coefficient Default = 1.0 (Real)
VISC	Maximum viscosity. See comment 15. Default = 1030 (Real)
TOL	Tolerance on principal direction update Default = 1.0 (Real)
TIDLi	Identification number of a TABLES1 Bulk Data Entry that defines the loading yield stress vs. plastic strain curve i corresponding to EPSRi. Separate functions must be defined for different strain rates. No default (Integer > 0)
TIDUi	Identification number of a TABLES1 that defines the unloading yield stress vs. plastic strain curve "i" corresponding to EPSRi. Separate functions must be defined for different strain rates. Unloading functions TIDUi are used only if the unloading curve TIDUN is not defined. = 0: the TIDL1 curve is used for the corresponding unloading process No default (Integer > 0)
FSCAi	Scale factor for TIDLi and TIDUi Default = 1.0 (Real)
EPSRi	Strain rate(s) for TIDLi and TIDUi Note: EPSRi is (are) referred to as in the comments. (Real)

Comments

1.	The material identification number must be that of an existing MAT1 bulk data entry. Only one MATXi material extension can be associated with a particular MAT1.

2.	MATX38 is only applied in geometric nonlinear analysis subcases which are defined by ANALYSIS = EXPDYN. It is ignored for all other subcases.

3.	Nominal stresses are computed by interpolation from input functions: , for given , read two values of functions with immediate availability for the two immediately lower and higher strain rates.

Example below is for two strain rate curves (up to five may be input).ou

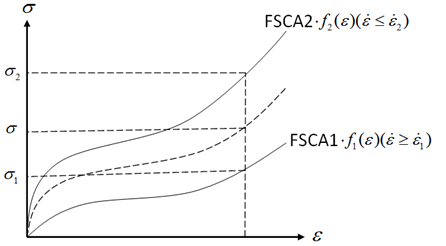
matx38

The interpolation function is defined as:

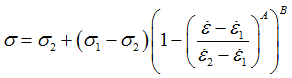
Where, , and input are positive in compression, and refers to the ESPRi stain rate data.

The parameters A and B define the shape of the interpolation function within each interval. If A = B = 1, the interpolation is linear.

The curves are always nominal stresses versus engineering strains.

4.	If E0 is not defined, E on MAT1 card is used instead; if NUC is not empty, NU on the MAT1 card is used instead.

5.	The strain is negative in compression. The tensile stress can either be negative or positive. The absolute stress value is used in the material law.

6.	A “coupled” set of principal nominal stresses is computed with anisotropic Poisson’s ratios:

in tension (), and in compression.

Where,

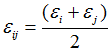
7.	IFLAG = 1: For compression, Young Modulus E0 and Poisson's ratio NUC are used. Whereas, in tension the instantaneous Young modulus ratio ET is used. The other data is ignored (especially, no viscous effect can be expected).

8.	Hysteresis is only applied in compression, using the relation:

9.	When KAIR = 1:

If NP ≠ 0:

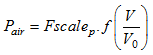, where f refers to the function number NP.

If NP = 0:

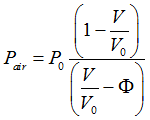
Relaxation is applied as .

Where, RP is the relaxation rate of pressure and t is the time.

10.	If the unloading curve is not defined (TIDUN=blank) when unloading, then TIDUi are used. If both TIDUN and TIDUi are not defined, then is computed from loading curve one (TIDL1).

11.	If the unloading curve (TIDUN/TIDUi) is defined, is interpolated between curve 1 (TIDUL1) and curve TIDUN. In this case, curve 1 (TIDUL1) must correspond to a quasi-static state.

12.	If TIDUN > 0 and the unloading strain rate is equal to the quasi-static curve 1 (TIDUL1), the TIDUN curve is used for unloading.

13.	E0 < E < EFINAL

EFINAL is the absolute value of the strain corresponding to the maximum compression modulus.

14.	The instantaneous modulus is only used for tension.

15.	If VISC is input, interpolated stress will be limited by this value to have a larger timestep:

16.	The behavior is strain rate independent when the stress function interpolation is conducted for a queried strain rate () that is lower than the strain rate specified via EPSR1 (), and strain rate independence occurs, if .

17.	This card is represented as a material in HyperMesh.