MATX42

Bulk Data Entry

MATX42 – Material Property Extension for Ogden, Mooney-Rivlin Material for Geometric Nonlinear Analysis

Description

Defines additional material properties for Ogden, Mooney-Rivlin material for geometric nonlinear analysis. This material is used to model rubber, polymers, and elastomers.

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MATX42	MID	SCUT		TBID	FBULK
	LAW	MU1	ALFA1	MU2	ALFA2	MU3	ALFA3
		MU4	ALFA4	MU5	ALFA5

Optional continuation lines for prony value:

	PRONY	G1	T1	G2	T2	G3	T3
		G4	T4	G5	T5	...

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
MAT1	102	10.0		0.495	6.0E-10
MATX42	102
	LAW	0.10	2.0	-0.010	-2.0

Field	Contents
MID	Material ID of the associated MAT1. See comment 1. No default (Integer > 0)
SCUT	Cut-off stress in tension. Default = 1030 (Real > 0)
TBID	Identification number of a TABLES1 to define the bulk function f(J) that scales the bulk modulus vs. relative volume. If TBID = 0, f(J) = const. = 1.0. Default = 0 (Integer > 0)
FBULK	Scale factor for bulk function. Default = 1.0 (Real > 0)
LAW	Indicates that material parameters MUi and ALFAi follow.
MUi	Parameter μi. Up to five pairs are permitted. (Real)
ALFAi	Parameter αi. Up to five pairs are permitted. (Real)
PRONY	Indicates that prony model parameters Gi and Ti follow.
Gi	Parameters Gi for prony model (Comments 7 and 8) (Real)
Ti	Parameter Ti for prony model (Comments 7 and 8) (Real)

Comments

1.	The material identification number must be that of an existing MAT1 bulk data entry. Only one MATXi material extension can be associated with a particular MAT1.

2.	MATX42 is only applied in geometric nonlinear analysis subcases which are defined by ANALYSIS = EXPDYN. It is ignored for all other subcases.

3.	The recommended Poisson’s ratio for incompressible material is NU = 0.495. NU is defined on the corresponding MAT1.

4.	The strain energy density W is computed using the following equation:

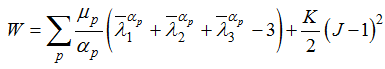
mat42_equation1

Where, is the ith principal engineering stretch (, is the ith principal engineering strain). The Cauchy stress is computed as follows:

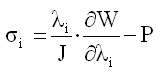
matx42_2

with J = λ1 * λ2 * λ3 being the relative volume:

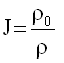
matx42_3

The quantity, P is the pressure:

P = K * FBULK * f (J) * (J - 1)

The Bulk Modulus, K is:

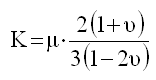
matx42_4

with the ground shear modulus μ:

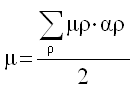
matx42_5

5.	An incompressible Mooney-Rivlin material is governed by:

W = C10 (I1 - 3) + C01 (I2 - 3)

where, Ii is ith invariant of the right-hand Cauchy-Green Tensor. It can be modeled using the following parameters:

μ1 = 2 * C10

μ2 = -2 * C01

α1 = 2.0

α2 = -2.0

6.	Coefficients of the Prony series (Gi, Ti ) are used to describe viscous effects using the Maxwell model (which can be described in a simplified manner as a system of n springs with stiffness' Gi and dampers ηi):

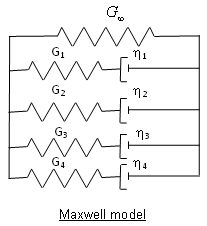
law82_maxwell_model

The hyperelastic ground shear modulus, is exactly the long-term shear modulus G∞ in the Maxwell model, and Ti is the relaxation time:

The Gi and Ti values must be positive.

7.	Viscous effects are modeled through a convolution integral using Prony series. This is an extension of small strain theory (described in comment 6) to large nonlinear strain case. The Kirchhoff viscous stress is given by:

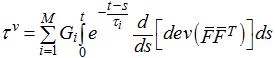
matlaw42_eq5

with, F being the deformation gradient matrix, and denotes the deviatoric part of tensor .

The viscous-Cauchy stress is written as:

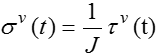
matlaw42_eq6

8.	This card is represented as a material in HyperMesh.