|
»Click here to display Table of Contents«
|
MATX43 |
|
|
|
|
|
MATX43 |
|
|
|
|
|
»Click here to display Table of Contents«
|
MATX43 |
|
|
|
|
|
MATX43 |
|
|
|
|
Bulk Data Entry
MATX43 – Material Property Extension for Hill Orthotropic Material for Geometric Nonlinear Analysis
Description
Defines additional material properties for Hill Orthotropic material for geometric nonlinear analysis. This law is only applicable to two-dimensional elements.
Format
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
(10) |
MATX43 |
MID |
R00 |
R45 |
R90 |
CHARD |
EPSPF |
EPST1 |
EPST2 |
|
If strain rate dependent material, at least 1 time, at most 10 times
|
TID1 |
FSCA1 |
EPSR1 |
|
|
|
|
|
|
|
TID2 |
FSCA2 |
EPSR2 |
|
|
|
|
|
|
|
… |
… |
… |
|
|
|
|
|
|
|
Field |
Contents |
MID |
Material ID of the associated MAT8. See comment 1. No default (Integer > 0) |
R00 |
Lankford parameter at 0 degree. Default = 1.0 (Real) |
R45 |
Lankford parameter at 45 degrees. Default = 1.0 (Real) |
R90 |
Lankford parameter at 90 degrees. Default = 1.0 (Real) |
CHARD |
Hardening coefficient. 0.0 - The hardening is a full isotropic model. Default = 0.0 (1.0 > Real > 0.0) |
EPSPF |
Failure plastic strain. Default = 1030 (Real) |
EPST1 |
Tensile failure strain. Default = 1030 (Real) |
EPST2 |
Tensile failure strain. Default = 2.0*1030 (Real) |
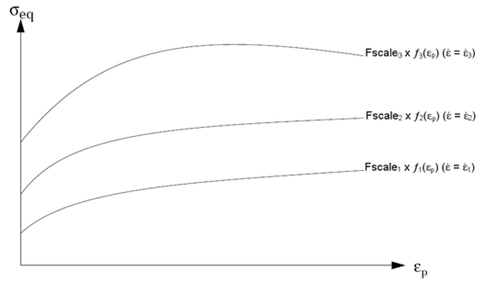
TIDi |
Identification number of a TABLES1 that defines the yield stress vs. plastic strain function corresponding to EPSRi. Separate functions must be defined for different strain rates. Integer > 0 |
FSCAi |
Scale factor for ith function. Default= 1.0 (Real) |
EPSRi |
Strain rate for ith function. (Real) |
| 1. | The material identification number must be that of an existing MAT8 bulk data entry. Only one MATX43 material extension can be associated with a particular MAT8. E1 must be equal to E2 on MAT8 that is extended by MATX43. |
| 2. | MATX43 is only applied in geometric nonlinear analysis subcases which are defined by ANALYSIS = EXPDYN. It is ignored for all other subcases. |
| 3. | The yield stress is defined by a user function and the yield stress is compared to equivalent stress. |
| 4. | Angles for Lankford parameters are defined with respect to orthotropic direction 1. |
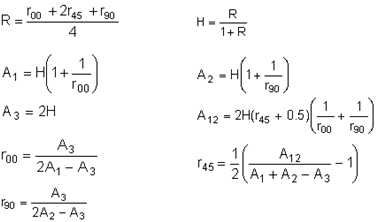
| 5. | The Lankford parameters rα are determined from a simple tensile test at an angle α to the orthotropic direction 1. |
| 6. | If the last point of the first (static) function equals 0 in stress, default value of failure plastic strain EPSPF is set to the corresponding value of plastic strain, p. |
| 7. | If plastic strain εp reaches failure plastic strain εpmax, the element is deleted. |
| 8. | If ε1 (largest principal strain) > εt1(EPST1), stress is reduced according to the following relation: |
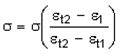
| 9. | If ε1 (largest principal strain) > εt2(EPST2), the stress is reduced to be 0 (but the element is not deleted). If  (EPSRn), yield is interpolated between ƒn and ƒn-1. If  (EPSR1), function ƒ1 is used. Above  , yield is extrapolated. |
| 10. | This card is represented as extension to a MAT8 material in HyperMesh. |
See Also:
