11.2 - Strain Rate Effect |

|

|

|

|
|
11.2 - Strain Rate Effect |

|

|

|

|
TitleStrain rate effect |
|
||||||
Number11.2 |
|||||||
Brief DescriptionThe strain rate effect is taken into account, using filtering (cut-off frequency). |
|||||||
Keywords
|
|||||||
RADIOSS Options
|
|||||||
Input FileTime_History_files: <install_directory>/demos/hwsolvers/radioss/11_Tensile_Test/TENSILET01 |
|||||||
Technical / Theoretical LevelAdvanced |
|||||||
In this additional study, the Johnson-Cook model is used to study the strain rate influence on stress with or without filtering. There is no comparison with the experiment data in this section. The study of sensitivity will be performed up to the beginning of the necking point.
| • | Stress-strain relationship: |
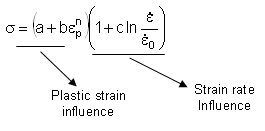
The Johnson-Cook plasticity model will take into account the strain rate effect on the elasto-plastic material behavior in order to improve the quality of simulation.
The law reads as follows:
where:
![]() is the strain rate
is the strain rate
![]() 0 is the reference strain
0 is the reference strain
![]() p is the plastic strain (true strain)
p is the plastic strain (true strain)
c is the strain rate coefficient
The two optional inputs, strain rate coefficient and reference strain rate must be defined for the material. The purpose of the sensitivity study is to illustrate the influence of material parameters.
For further explanations about the Johnson-Cook model, refer to "Elasto-plasticity of Isotropic Materials" in the RADIOSS Theory Manual.
Because of the numerical application of dynamic loadings, the strain rates cause high frequency vibrations, which are not physical; thus the stress/strain curves look "noisy". To obtain smooth results, the strain rate filtering option will allow the reduction of those oscillations by removing the high frequency vibrations. A cut-off frequency for strain rate filtering (Fcut) is used since its value has to be smaller than half of the sampling frequency (1/![]() t).
t).
In this example, ![]() t = 0.2163x10-3 ms.
t = 0.2163x10-3 ms.
The constants a, b and n which define the shape of the stress/strain curve are:
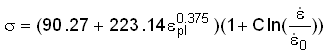
a = 90.27 MPa
b = 223.14 MPa
n = 0.375
The results are reported in the following tables.
The influence of the strain rate and stress smoothing are shown below (with ![]() = 5x10-3 ms-1 and c = 0.1):
= 5x10-3 ms-1 and c = 0.1):
Stress Comparison |
|---|
|
Influence of the Cut-off Frequency for Smoothing |
|---|
|
The following results show the effect of the reference strain rate, ![]() and strain rate coefficient, c:
and strain rate coefficient, c:
Influence of the Reference Strain Rate |
|---|
|
Influence of the Strain Rate Coefficient, c |
|---|
|
Results are smoothed with correct cut-off frequencies.
Figure 36 compares the distribution of the first principal strain rate in the object, with and without strain rate filtering.
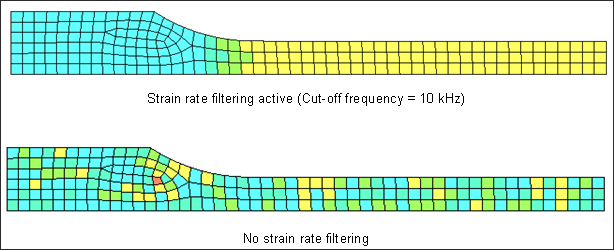
Fig 36: First principal strain rate comparison at time t=4 ms.
A more physical strain rate distribution is achieved by filtering. Moreover, such results show spatial oscillations when not damped by filtering. The explicit scheme is an element-by-element method and the local treatment of temporal oscillations puts spatial oscillations into the model.
| • | Strain rate coefficient c influence: |
If c is set to zero, the strain rate effect is not taken into account. This coefficient affects the yield stress and it slightly translates curves in the plastic region. It must be adjusted in accordance with the reference strain rate.
| • | Reference strain rate |
If the strain rate is lower than the reference strain rate, there is no strain rate effect. Therefore, the lower the reference strain rate, the more the effect will be emphasized. The effect appears as a translation of the curve towards higher stresses. An increase in the flow stress using an increasing reference strain rate is observed.
| • | Cut-off frequency influence: |
The cut-off frequency must not be set higher than half of the sampling frequency. Smoothing is improved as the cut-off frequency comes closer to a particular value and the convergence of the curve until a smoothing curve can be observed. A high-reference strain rate requires low cut-off frequencies.
A tensile test is simulated using several material laws in RADIOSS. A method is set up to correspond to the material parameters in the Johnson-Cook model. The rupture phase is very sensitive and the simulation results strongly depend upon the starting point for necking. The point-by-point definition of the hardening curve in law 36 enables to bypass the adaptation difficulties when using the Johnson-Cook model. However, the results following the necking point are very sensitive to the position of points defining the hardening curve.
A method to filter the strain rate is also demonstrated. The method can be generalized to the industrial cases.