Example 24 - Laminating |

|

|

|

|
|
Example 24 - Laminating |

|

|

|

|
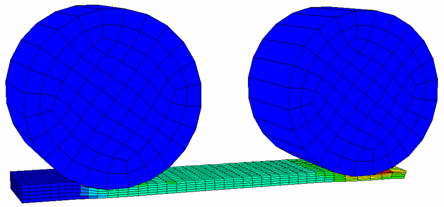
The lamination of a metal strip under two rolling cylinders is studied. Several formulations are compared. Large and small strain assumptions are respectively used. The influence of the number of elements concerning the thickness of the metal strip, as well as element formulation is discussed.
TitleLaminating |
|
||||||||||||
Number24.1 |
|||||||||||||
Brief DescriptionTwo rolling rigid cylinders squeeze a plate to laminate it. |
|||||||||||||
Keywords
|
|||||||||||||
RADIOSS Options
|
|||||||||||||
Input FileThickness: 2 elements: <install_directory>/demos/hwsolvers/radioss/24_Laminating/Thickness/2_elements/ROLLING* 5 elements: //.../radioss/24_Laminating/Thickness/5_elements/ROLLING* Formulation: Isolid=12: <install_directory>/demos/hwsolvers/radioss/24_Laminating/Formulation/Isolid12/ROLLING* Icpre=0: //.../radioss/24_Laminating/Formulation/Icpre0/ROLLING* Icpre=1: //.../radioss/24_Laminating/Formulation/Icpre1/ROLLING* Temperature: T=800°C: <install_directory>/demos/hwsolvers/radioss/24_Laminating/temperature/T=800/ROLLING* T=1200°C: //.../radioss/24_Laminating/temperature/T=1200/ROLLING* |
|||||||||||||
Technical / Theoretical LevelAdvanced |
|||||||||||||
This analysis shows a phase of a rail rolling. A metal strip is successively passed through two rollers aiming at reducing its thickness. Both rollers have a constant angular velocity of 6.85 rad/s, and the metal strip is dragged along a moving machine bed. This process may be considered quasi-static and involves high deformation (mainly compression).
Units: mm, s, Mg, N, MPa
Both rollers and the metal strip are made of mild steel. They exhibit an isotropic elasto-plastic behavior which can be modeled using the Johnson-Cook law (/MAT/LAW2):
| • | Initial density: 7.8 x 109 Mg/mm3 |
| • | Young modulus: 210000 MPa |
| • | Poisson ratio: 0.3 |
| • | Yield stress: 170 MPa |
| • | Hardening parameter: 400 MPa |
| • | Hardening exponent: 0.475 |
| Note: | Any temperature influence will not be taken into account. The problem is studied using the following parameters: |
| • | Temperature exponent: 1 |
| • | Melting temperature: 2073 K (around 1800°C) |
| • | Specific heat at constant pressure Cp: 460 J/Kg.K |
| • | Geometry: The metal strip has a cross-section of 80 x 20 mm and the rollers have a radius of 100 mm. After the passage of the first roller, the thickness is reduced by 7 mm, then by another 5 mm after the second roller. |
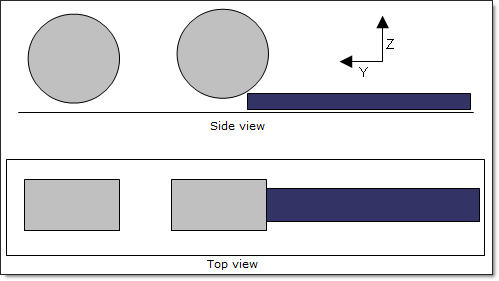
Fig 1: Geometry of the problem.
It is not necessary to pass many elements over the width of the metal strip, but rather to obtain an accurate stress distribution over its thickness by passing a minimum of five elements over the thickness of the metal strip. Depending on what is being looked for, passing five elements over the thickness may seem like a lot. This issue should be discussed in the early part of the analysis. Concerning the rollers as the elements is of first order, as it is not easy to perfectly model the curvature. The mesh must be fine enough to estimate the curvature with as much accuracy as possible, one element over the width being sufficient.
Some details are made: The moving machine bed is not modeled and all lower nodes of the metal strip are constrained in the Z-direction. Moreover, an initial velocity is applied to the metal strip to initiate contact with the first roller. Assuming there is a Coulomb friction between the metal strip and the roller using a friction coefficient of 0.3, the metal strip is then dragged by the roller.
Assuming the rollers are rigid, a constant angular velocity to the master nodes is applied.
As this process may be considered as a quasi-static one, the density is artificially increased by a factor of 10000, that the density used is now 7.8 x 10-5. Consequently, the time step will be higher, and assuming the kinetic energy is negligible compared to the energy of deformation, results will be correct.
| Note: | Density can be increased as long as dynamic effects are negligible. |
| • | Boundary conditions: |
The lower nodes of the metal strip are constrained in Z (to represent the moving machine bed).
The master nodes of the rollers are constrained in all directions, except rotation around the X-axis.
| • | Imposed velocity: |
A constant angular velocity around the X-axis is applied to both of the rollers’ master nodes.
| • | Initial velocity: |
An initial velocity of 500 mm/s in the X-direction is applied to every node of the metal strip.
| • | Interfaces: |
Contact between the metal strip and the rollers are modeled by a type 7 interface. The master surface is defined by the external surface of the rollers, and the slave nodes by the metal strip (/GRNOD/PART). As there is only one element over the width of the rollers. The previous interface does not need to be symmetrically arranged. The gap is chosen arbitrarily at 1 mm.
It was mentioned earlier that passing five elements over the thickness is a minimum; but how was that number reached? It is not an easy question, as this number depends on what is being looked for. If interested in the stress distribution over the thickness, the higher the better; thus the choice would be a trade-off between accuracy and the CPU time. Compare the von Mises stress and the plastic strain for two elements over the thickness using one integration point (Isolid =1) and five elements with 8 integration points (Isolid =12).
Table 1: Comparison between two and five elements.
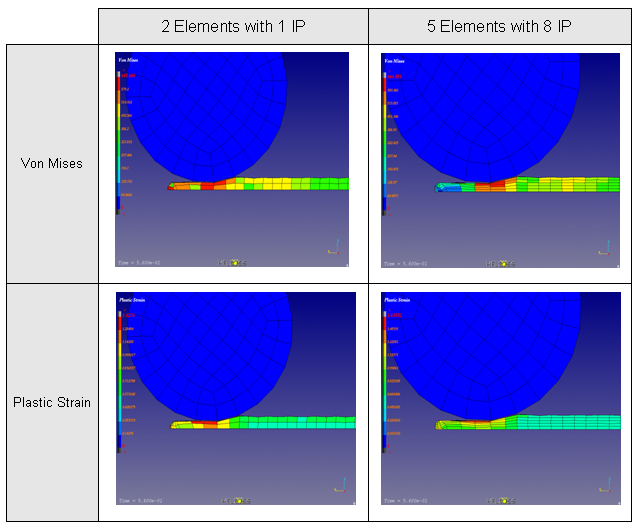
Passing two elements over the thickness is not enough to see the stress (or strain) distribution; five elements is enough though. If the deformed shape is not smooth and/or the gradient between the two elements is too high, consider refining the mesh; however, this can be somewhat costly! Additionally, it takes 12 times longer to run the model with five elements over the width.
What if the only interest is in the reaction force acting on the cylinder?
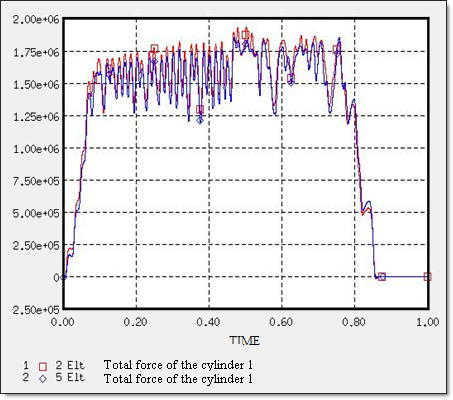
Fig 2: Reaction forces acting on the cylinder.
The above graph indicates the reaction force on the first cylinder using two or five elements over the thickness. Both curves are almost identical and it takes much longer to use five elements. Thus, to save CPU time, there is no need to use more than two elements.
Usually for problems involving large deformations, a large strain formulation would be used. In RADIOSS this is the default setting, but it is also possible to use a small strain formulation. This formulation is not very accurate for large deformations, but it is more robust and enables the time step to not decrease too much. Indeed, large deformation/rotation problems may lead to mesh distortion which causes the time step to drop drastically; computation may even stop due to a negative volume. The small strain formulation overcomes all this by assuming a constant volume, consequently the time step becomes constant, and even if the mesh is completely distorted, computation will not be stopped due to the negative volume.
This formulation can be applied from t=0 by setting the flag Ismstr to 1, directly in the type of a specific part. It is also possible to switch from a large strain formulation to a small strain formulation during the simulation in order to prevent a negative volume and/or to maintain a decent time step using the /DT/BRICK/CST option in the Engine file (*_0001.rad) having a critical time step.
In this example the results between a full large strain formulation, a full small strain formulation and a "mixed formulation” using /DT/BRICK/CST are compared. The average time step is 20% higher for a full small strain formulation and 3.5% higher for a "mixed formulation” in comparison to the default large strain formulation. Thus, there is a significant gain in terms of CPU time using the small strain formulation. The deformed shape is not good (Table 2).
Table 2: Deformed shape.
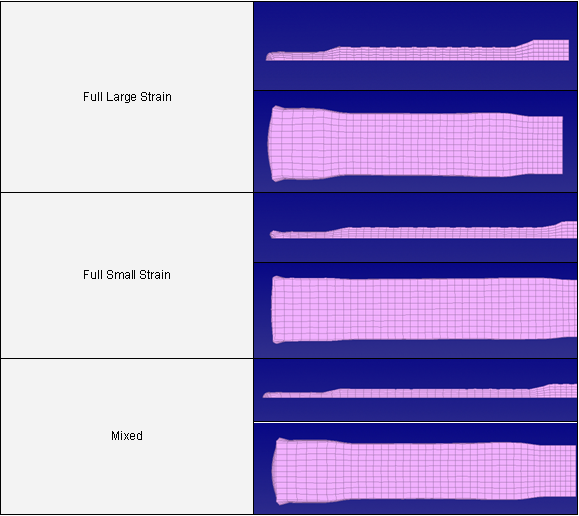
Moreover, looking at the plastic strain, using a small strain formulation from t=0 leads to major errors (Table 3). First of all, the strain distribution is not well determined and most importantly, the maximum is far too low, which means permanent deformation was under-estimated.
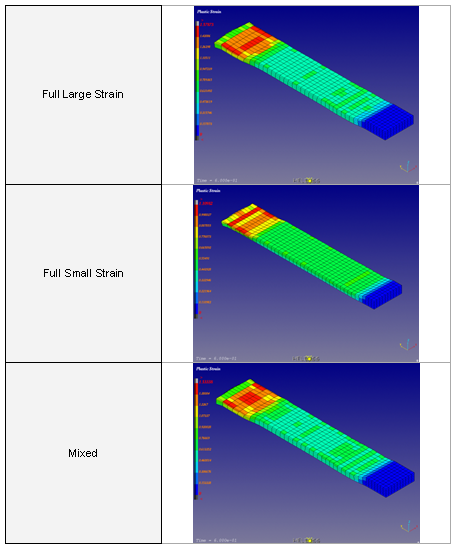
In such a case, it may be of interest to use the small strain formulation but only for a few elements reaching a critical time step (using /DT/NODA/CST); as the time step will not stop, due to a distorted element. However, for accuracy reasons, the number of elements switching to a small strain formulation should be checked, the lower the better.
The improved solid formulation HA8 overcomes the drawbacks of the standard 8 integration points’ formulation (Isolid=12 or 14). In particular, in the case of a pure bend, "shear-locking”, which makes the standard formulation rather stiffer, does not exist. It is also possible to use the small strain formulation, which contrary to the 8 integration points’ formulation is not compatible. It is now possible to use up to 9 integration points for each direction.
Depending on the value given for the Icpre flag, the HA8 formulation may use a reduced pressure integration. In this part the influence of this flag on simulation will be investigated in order to find out the most suitable value. Table 4 shows both the deformed shape and the equivalent plastic strain for the different solid formulations. The new HA8 formulation with reduced pressure integration behaves the same way as the standard 8 integration points formulation. If the reduced pressure integration is not activated, the results will not be correct, with the metal strip deforming badly and the plastic strain being over-estimated (Table 4). The reaction force acting on the cylinder will also be over-estimated (Table 3), which means that the structure will be stiffer without the reduced pressure integration.
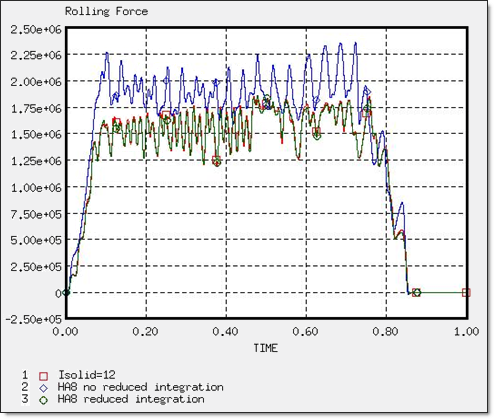
Fig 3: Rolling Force for different formulations
Table 4: Plastic Strain for different formulations.
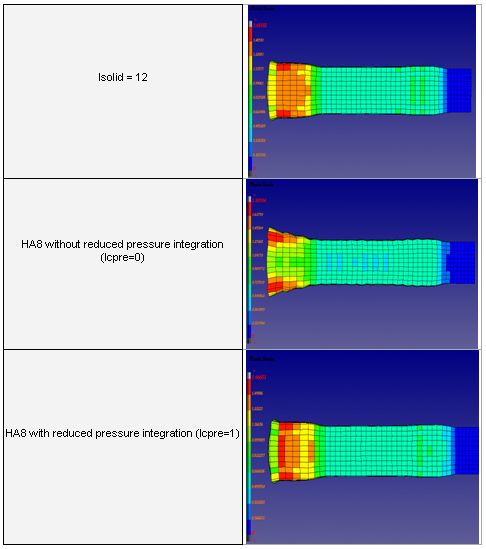
The HA8 formulation must always be used with reduced pressure integration, the only time when this option must be deactivated is in the case of emulating a thick shell formulation with 8-nodes bricks.
When metal forming, one of the main parameters engineers' study whether the force is needed during the process. In this particular case, it concerns the rolling force applied by the cylinders. Engineers try to minimize this force in order to use less power and to reduce maintenance on the cylinders. One way to do so is to form metal at a higher temperature. RADIOSS takes into account the temperature dependency using the same law already used (Johnson-Cook law). The following diagram indicates the rolling force in accordance with the temperature and, as expected the higher the temperature, the lower the force. Consequently, metal forming is a trade-off between the power saved using a lower force and the power required to raise the temperature.
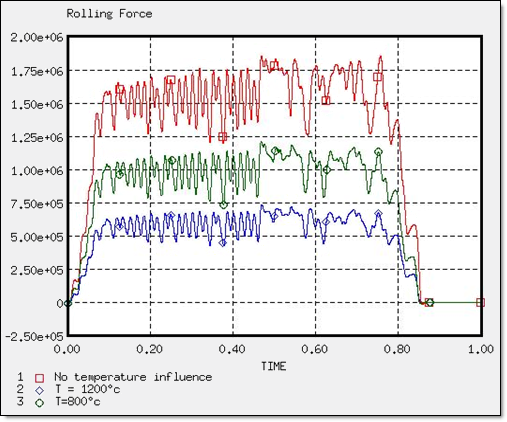
Fig 4: Rolling Force.
The squeezing of the metal strip below two rolling cylinders is simulated by RADIOSS. The large deformation formulation, when a sufficient number of elements are used, obtaining physically-acceptable results is allowed. The small strain option leads to bad results, but with low cost. The element formulation and the number of integration points through thickness are other parameters influencing results; the higher the precision, the higher the cost. On the other hand, as the problem is considered to be quasi-static, resolution using the RADIOSS implicit solver can be envisaged.