PCNTX20

Bulk Data Entry

PCNTX20 – Extended CONTACT Property type 20 for Geometric Nonlinear Analysis

Description

Defines properties type 20 of a CONTACT interface for geometric nonlinear analysis.

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
PCNTX20	PID	ISYM	IEDGE	GRNDID				EDGEAngle
				IGAP		IBAG	IDEL
				FPENMAX
	STFAC	FRIC	GAP	TSATAT	TEND
	IBC			INACTI	VISS	VISF
	IFRIC	IFILT	FFAC	IFORM
	FRICDAT	C1	C2	C3	C4	C5	C6

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
PCONT	34
PCNTX20	34

Field	Contents
PID	Property identification number of the associated PCONT. No default (Integer > 0)
ISYM	Symmetric contact flag. Default as defined by CONTPRM (Character = SYM or UNSYM) SYM – Symmetric contact. UNSYM – Master-slave contact. If SSID defines a grid set, the contact is always a master-slave contact.
IEDGE	Flag for edge generation from slave and master surfaces. Default as defined by CONTPRM (Character = NO, ALL, BORD, or FEAT) NO – No edge generation. All – All segment edges are included. BORD – External border of slave and master surface is used. FEAT – External border as well as features defined by FANG are used.
GRNDID	Optional nodes group identifier (Integer).
EdgeAngle	Edges angle (used only if IEDGE = FEAT) Default = 91 (Real) If angle between two edges is smaller than EdgeAngle, the edge is considered.
IGAP	Gap definition flag. Default as defined by CONTPRM (Character = CONST or VAR) CONST - Gap is constant and equal to GAP (See comment 6). VAR - Gap is variable (in space, not in time) according to the characteristics of the impacting surfaces and nodes (See comment 7).
IBAG	Airbag vent holes closure flag in case of contact. Default = 0 (Integer) 0 - No closure. 1 - Closure.
IDEL	Flag for node and segment deletion. Default as defined by CONTPRM (Integer = 0, 1, or 2) 0 - No deletion. 1 - When all the elements (shells and solids) associated to one segment are deleted, the segment is removed from the master side of the interface. Additionally, non-connected nodes are removed from the slave side of the interface. 2 - When a shell or a solid element is deleted, the corresponding segment is removed from the master side of the interface. Additionally, non-connected nodes are removed from the slave side of the interface.
FPENMAX	Maximum initial penetration factor (0 < FPENMAX < 1) (See comment 8). Default = 1.0 (Real)
STFAC	Interface stiffness scale factor. Default as defined by CONTPRM (Real > 0)
FRIC	Coulomb friction. Default as defined by CONTPRM (Real > 0)
GAP	Gap for impact activation (See comments 4 and 6). Default as defined by CONTPRM (Real > 0)
TSTART	Start time. Default = 0.0 (Real > 0)
TEND	Time for temporary deactivation. Default = 1030 (Real > 0)
IBC	Flag for deactivation of boundary conditions at impact applied to the slave grid set. Default as defined by CONTPRM (Character = X, Y, Z, XY, XZ, YZ, or XYZ)
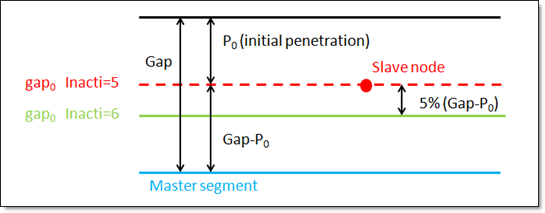
INACTI	Handling of initial penetrations flag (See comment 9). Default as defined by CONTPRM (Integer = 0, 1, 2, 3, or 5) 0 - No action. 1 - Deactivation of stiffness on nodes. 2 - Deactivation of stiffness on elements. 3 - Change slave node coordinates to avoid small initial penetrations. 5 - Gap is variable with time but initial gap is slightly de-penetrated as follows: gap0 = gap - P0 – 0.05 * (gap - P0) Valid in explicit analysis: 0, 1, 2, 3 and 5. Invalid entries are ignored.
VISS	Critical damping coefficient on interface stiffness. Default as defined by CONTPRM (Real > 0)
VISF	Critical damping coefficient on interface friction. Default as defined by CONTPRM (Real > 0)
IFRIC	Friction formulation flag (See comment 10). Default as defined by CONTPRM (Character = COUL, GEN, DARM, REN) COUL - Static Coulomb friction law. GEN - Generalized viscous friction law. DARM - Darmstad friction law. REN - Renard friction law.
IFILT	Friction filtering flag (See comment 11). Default as defined by CONTPRM (Character = NO, SIMP, PER, or CUTF) NO - No filter is used. SIMP - Simple numerical filter. PER - Standard -3dB filter with filtering period. CUTF - Standard -3dB filter with cutting frequency.
FFAC	Friction filtering factor. Default as defined by CONTPRM (Real = 0.0 < FFAC < 1.0)
IFORM	Type of friction penalty formulation (See comment 12). Default as defined by CONTPRM (Character = VISC or STIFF) VISC - Viscous (total) formulation. STIFF - Stiffness (incremental) formulation.
FRICDAT	Indicates that additional information for IFRIC will follow. Only available when IFRIC = GEN, DARM or REN.
C1, C2, C3, C4, C5, C6	Coefficients to define variable friction coefficient in IFRIC = GEN, DARM, or REN. Default as defined by CONTPRM (Real > 0)

Comments

1.	The property identification number must be that of an existing PCONT bulk data entry. Only one PCNTX20 property extension can be associated with a particular PCONT.

2.	PCNTX20 is only applied in geometric nonlinear explicit dynamic analysis subcase which is defined by ANALYSIS = EXPDYN. It is ignored for all other subcases.

3.	If FRIC is not explicitly defined on the PCONTX/PCNTX# entries, the MU1 value on the CONTACT or PCONT entry is used for FRIC in the /INTER entries for Geometric Nonlinear Analysis. Otherwise, FRIC on PCONTX/PCNTX# overwrites the MU1 value on CONTACT/PCONT.

4.	In implicit analysis, different contact formulations are used for contact where slave and master set do not overlap and where they overlap (self-contact).

In the case of self-contact, the gap cannot be zero and a constant gap is used. For small initial gaps, the convergence will be more stable and faster if GAP is larger than the initial gap.

In implicit analysis, sometimes a stiffness with scaling factor reduction (for example, STFAC = 0.01) or reduction in impacted thickness (if rigid one) might reduce unbalanced forces and improve convergence, particularly in shell structures under bending where the effective stiffness is much lower than membrane stiffness; but it should be noted that too low of a value could also lead to divergence.

5.	If ISTF ≠ 1, the interface stiffness K is computed from the master segment stiffness Km and/or the slave segment stiffness Ks.

The master stiffness is computed from Km = STFAC * B * S * S/V for solids, Km = 0.5 * STFAC * E * t for shells.

The slave stiffness is an equivalent nodal stiffness computed as Ks = STFAC * B * V-3 for solids, Ks = 0.5 * STFAC * E * t for shells.

In these equations, B is the Bulk Modulus, S is the segment area, and V is the volume of a solid. There is no limitation to the value of stiffness factor (but a value larger than 1.0 can reduce the initial time step).

The interface stiffness is K = max (STMIN, min (STMAX, K1)) with:

•	ISTF = 0, K1 = Km

•	ISTF = 2, K1 = 0.5 * (Km + Ks)

•	ISTF = 3, K1 = max (Km, Ks)

•	ISTF = 4, K1 = min (Km, Ks)

•	ISTF = 5, K1 = Km * Ks / (Km + Ks)

6.	The default for the constant gap (IGAP = CONST) is the minimum of:

•	t, average thickness of the master shell elements

•	l/10, l – average side length of the master solid elements

•	lmin/2, lmin – smallest side length of all master segments (shell or solid)

7.	The variable gap (IGAP = VAR) is computed as: gs + gm

with:

•	gm - master element gap with

gm = t/2, t: thickness of the master element for shell elements.

gm = 0 for solid elements.

•	gs - slave node gap:

gs = 0 if the slave node is not connected to any element or is only connected to solid or spring elements.

gs = t/2, t - largest thickness of the shell elements connected to the slave node.

gs = 1/2√S for truss and beam elements, with S being the cross section of the element.

If the slave node is connected to multiple shells and/or beams or trusses, the largest computed slave gap is used.

8.	Maximum penetration value is set as a fraction of the actual gap (including variable gap):

Penmax = FPENMAX * gap

If the initial penetration of a slave node is greater than the calculated maximum value (Penmax), the node will be deactivated from the interface (node stiffness deactivation).

9.	INACTI = 3, is only recommended for small initial penetrations and should be used with caution because:

•	the coordinate change is irreversible

•	it may create other initial penetrations if several surface layers are defined in the interfaces

•	it may create initial energy if the node belongs to a spring element

INACTI = 5 works as follows:

Inacti_flag_6

10.	IFRIC defines the friction model.

IFRIC = COUL – Coulomb friction with FT < FRIC * FN.

For IFRIC > 0, the friction coefficient is set by a function ()

where, p is the pressure of the normal force on the master segment and V is the tangential velocity of the slave node.

The following formulations are available:

•	IFRIC = 1 - Generalized viscous friction law

µ = FRIC + C1 * p + C2 * V + C3 * p * v + C4 * p2 + C5 * v2

•	IFRIC = 2 - Darmstad law

µ = C1 * e(C2V) * p2 + C3 * e(C4V) * p + C5 * e(C6V)

•	IFRIC = 3 - Renard law

	0 < V < C5
	C5 < V < C6
	C6 < V

where:

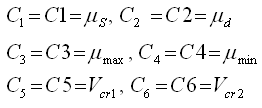
renard4

•	The first critical velocity Vcr1 must not be 0 (C5 ≠ 0). It also must be lower than the second critical velocity Vcr2 (C5 < C6).

•	The static friction coefficient C1 and the dynamic friction coefficient C2, must be lower than the maximum friction C3 (C1 < C3 and C2 < C3).

•	The minimum friction coefficient C4, must be lower than the static friction coefficient C1 and the dynamic friction coefficient C2 (C4 < C1 and C4 < C2).

11.	IFILT defines the method for computing the friction filtering coefficient. If IFILT ≠ NO, the tangential friction forces are smoothed using a filter:

FT = α * F'T + (1 - α) * F'T-1

where,

FT is the tangential force

F'T is the tangential force at time t

F'T-1 is the tangential force at time t-1

α is the filtering coefficient

IFILT = SIMP – α = FFAC

IFILT = PER – α = 2dt/FFAC, where dt/T = FFAC, T is the filtering period

IFILT = CUTF – α = 2 * FFAC * dt, where FFAC is the cutting frequency

12.	IFORM selects two types of contact friction penalty formulation.

The viscous (total) formulation (IFORM = VISC) computes an adhesive force as:

Fadh = VISF * √(2KM) * VT

FT = min (µFN, Fadh)

The stiffness (incremental) formulation (IFORM = STIFF) computes an adhesive force as:

Fadh = FTold + ΔFT

ΔFT = K * VT * dt

FTnew = min (µFN, Fadh)

13.	This card is represented as an extension to a PCONT property in HyperMesh.