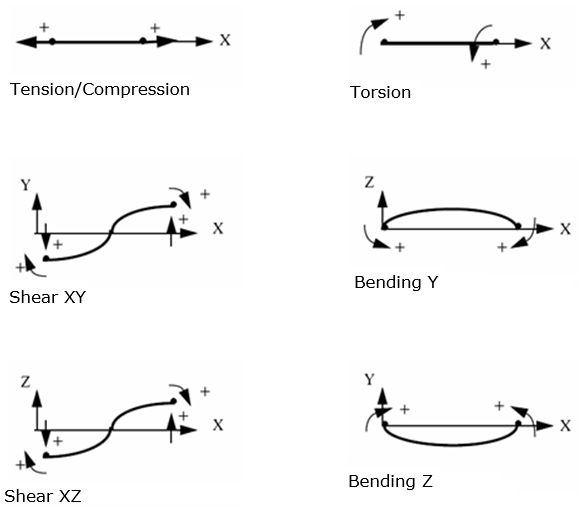
Field
|
Contents
|
SI Unit Example
|
prop_ID
|
Property identifier
(Integer, maximum 10 digits)
|
|
unit_ID
|
Optional unit identifier
(Integer, maximum 10 digits)
|
|
prop_title
|
Property title
(Character, maximum 100 characters)
|
|
Mass
|
Spring mass
(Real)
|
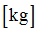
|
Inertia
|
Spring inertia
(Real)
|
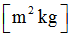
|
skew_ID
|
Skew system identifier
(Integer)
|
|
sens_ID
|
Sensor identifier
(Integer)
|
|
Isflag
|
Sensor flag (Comment 10)
(Integer)
=0: spring element activated
=1: spring element deactivated
=2: spring element activated or deactivated
|
|
Ifail
|
Failure criteria (Comment 8)
(Integer)
= 0: uni-directional criteria
= 1: multi-directional criteria
|
|
Ileng
|
Input per unit length flag
(Integer)
= 0: the force in the spring is computed as previously detailed formula (Comment 2)
= 1: all input are per unit length (Comment 3)
|
|
Ifail2
|
Failure model flag
Default = 0 (Integer)
= 0: old displacement criteria
= 1: new displacement criteria
= 2: force criteria
= 3: internal energy criteria
|
|
K1
|
Stiffness for tension
(Real)
|
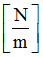
|
C1
|
Damping for tension/compression
(Real)
|

|
A1
|
Coefficient for strain rate effect in tension/compression
Default = 1.0 (Real)
|

|
B1
|
Coefficient for strain rate effect in tension/compression
(Real)
|

|
D1
|
Strain coefficients for elongation velocity for tension/compression
Default = 1.0 (Real)
|
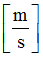
|
E1
|
Coefficient for strain rate effect in tension/compression
(Real)
|

|
Ascale1
|
Abscissa scale factor for 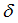 in tension/compression (fct_ID11 and fct_ID31) in tension/compression (fct_ID11 and fct_ID31)
(Real)
|
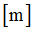
|
Hscale1
|
Coefficient for fct_ID41 in tension/compression
Default = 1 (Real)
|
|
fct_ID11
|
Function identifier defining 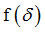 in tension/compression in tension/compression
If H1=4: Function identifier defining upper yield curve
(Integer)
= 0: for linear spring
|
|
H1
|
Hardening flag
(Integer)
= 0: Nonlinear elastic spring
= 1: Nonlinear elasto-plastic spring
= 2: Nonlinear elasto-plastic spring with decoupled hardening in tension and compression
= 4: Nonlinear elastic plastic spring “kinematic” hardening
= 5: Nonlinear elasto-plastic spring with nonlinear unloading
= 6: Nonlinear elasto-plastic spring with isotropic hardening and nonlinear unloading
= 7: Nonlinear spring with elastic hysteresis
|
|
fct_ID21
|
Function identifier defining 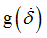 in tension/compression in tension/compression
(Integer)
|
|
fct_ID31
|
Function used only for unloading in tension/compression
If H1=4: Function identifier defining lower yield curve
If H1=5: Function identifier defining residual displacement vs maximum displacement
(Integer)
|
|
fct_ID41
|
Function identifier defining 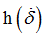 in tension/compression in tension/compression
(Integer)
|
|
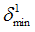
|
Negative failure limit
Default = -1030 (Real)
|
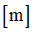
|
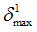
|
Positive failure limit
Default = 1030 (Real)
|
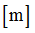
|
F1
|
Scale factor for 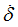 in tension/compression in tension/compression
(Real)
|
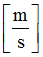
|
K2
|
Stiffness for shear XY
(Real)
|
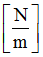
|
C2
|
Damping for shear XY
(Real)
|

|
A2
|
Coefficient for strain rate effect in shear XY
Default = 1.0 (Real)
|

|
B2
|
Logarithmic coefficient for strain rate effect in shear XY
Default = 1.0 (Real)
|

|
D2
|
Scale coefficients for shear velocity
Default = 1.0 (Real)
|
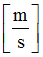
|
Ascale2
|
Abscissa scale factor for 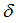 in shear XY (fct_ID12 and fct_ID32) in shear XY (fct_ID12 and fct_ID32)
(Real)
|
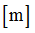
|
Hscale2
|
Coefficient for fct_ID42 in shear XY
Default = 1 (Real)
|
|
fct_ID12
|
Function identifier defining 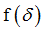 in shear XY in shear XY
If H2=4: Function identifier defining upper yield curve
(Integer)
= 0: linear spring
|
|
H2
|
Hardening flag
(Integer)
= 0: Nonlinear elastic spring
= 1: Nonlinear elasto-plastic spring
= 2: Nonlinear elasto-plastic spring with decoupled hardening in tension and compression
= 4: Nonlinear elastic plastic spring “kinematic” hardening
= 5: Nonlinear elasto-plastic spring with nonlinear unloading
= 6: Nonlinear elasto-plastic spring with isotropic hardening and nonlinear unloading
= 7: Nonlinear spring with elastic hysteresis
|
|
fct_ID22
|
Function identifier defining 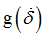 in shear XY in shear XY
(Integer)
|
|
fct_ID32
|
Function used only for unloading in shear XY
If H2 =4: Function identifier defining lower yield curve
If H2 =5: Function identifier defining residual displacement vs maximum displacement
(Integer)
|
|
fct_ID42
|
Function identifier defining 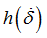 in shear XY in shear XY
(Integer)
|
|
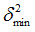
|
Negative failure limit
Default = -1030 (Real)
|
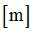
|
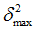
|
Positive failure limit
Default = 1030 (Real)
|
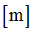
|
F2
|
Scale factor for 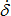 in shear XY in shear XY
(Real)
|
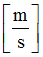
|
E2
|
Coefficient for strain rate effect in shear XY
(Real)
|

|
K3
|
Stiffness for shear XZ
(Real)
|
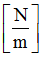
|
C3
|
Damping for shear XZ
(Real)
|

|
A3
|
Coefficient for strain rate effect in shear XZ
Default = 1.0 (Real)
|

|
B3
|
Logarithmic coefficient for strain rate effect in shear XZ
Default = 1.0 (Real)
|

|
D3
|
Scale coefficients for shear velocity
Default = 1.0 (Real)
|
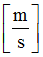
|
Ascale3
|
Abscissa scale factor for 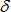 in shear XZ (fct_ID13 and fct_ID33) in shear XZ (fct_ID13 and fct_ID33)
(Real)
|
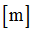
|
Hscale3
|
Coefficient for fct_ID43 in shear XZ
Default = 1 (Real)
|
|
fct_ID13
|
Function identifier defining 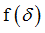 in shear XZ in shear XZ
If H3=4: Function identifier defining upper yield curve
(Integer)
= 0: linear spring
|
|
H3
|
Hardening flag
(Integer)
= 0: Nonlinear elastic spring
= 1: Nonlinear elasto-plastic spring
= 2: Nonlinear elasto-plastic spring with decoupled hardening in tension and compression
= 4: Nonlinear elastic plastic spring “kinematic” hardening
= 5: Nonlinear elasto-plastic spring with nonlinear unloading
= 6: Nonlinear elasto-plastic spring with isotropic hardening and nonlinear unloading
= 7: Nonlinear spring with elastic hysteresis
|
|
fct_ID23
|
Function identifier defining 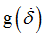 in shear XZ in shear XZ
(Integer)
|
|
fct_ID33
|
Function used only for unloading in shear XZ
If H3=4: Function identifier defining lower yield curve
If H3=5: Function identifier defining residual displacement vs maximum displacement
(Integer)
|
|
fct_ID43
|
Function identifier defining 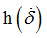 in shear XZ in shear XZ
(Integer)
|
|
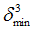
|
Negative failure limit
Default = -1030 (Real)
|
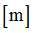
|
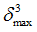
|
Positive failure limit
Default = 1030 (Real)
|
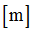
|
F3
|
Scale factor for 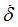 in shear XZ in shear XZ
(Real)
|
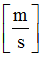
|
E3
|
Coefficient for strain rate effect in shear XZ
(Real)
|

|
K4
|
Stiffness for torsion
(Real)
|
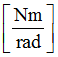
|
C4
|
Damping for torsion
(Real)
|
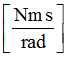
|
A4
|
Coefficient for strain rate effect in torsion (homogeneous to a moment)
Default = 1.0 (Real)
|

|
B4
|
Logarithmic coefficient for strain rate effect in torsion
(Real)
|

|
D4
|
Scale coefficients for torsion velocity
Default = 1.0 (Real)
|

|
Ascale4
|
Abscissa scale factor for 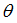 in torsion (fct_ID14 and fct_ID34) in torsion (fct_ID14 and fct_ID34)
(Real)
|

|
Hscale4
|
Coefficient for fct_ID44 in torsion
Default = 1 (Real)
|
|
fct_ID14
|
Function identifier defining 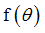 in torsion in torsion
If H4=4: Function identifier defining upper yield curve
(Integer)
= 0: linear spring
|
|
H4
|
Hardening flag
(Integer)
= 0: Nonlinear elastic spring
= 1: Nonlinear elasto-plastic spring
= 2: Nonlinear elasto-plastic spring with decoupled hardening in tension and compression
= 4: Nonlinear elastic plastic spring “kinematic” hardening
= 5: Nonlinear elasto-plastic spring with nonlinear unloading
= 6: Nonlinear elasto-plastic spring with isotropic hardening and nonlinear unloading
= 7: Nonlinear spring with elastic hysteresis
|
|
fct_ID24
|
Function identifier defining 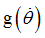 in torsion in torsion
(Integer)
|
|
fct_ID34
|
Function used only for unloading in torsion
If H4=4: Function identifier defining lower yield curve
If H4=5: Function identifier defining residual displacement vs maximum displacement
(Integer)
|
|
fct_ID44
|
Function identifier defining 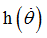 in torsion in torsion
(Integer)
|
|

|
Negative failure limit
Default = -1030 (Real)
|

|
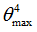
|
Positive failure limit
Default = 1030 (Real)
|

|
F4
|
Scale factor for 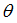 in torsion in torsion
(Real)
|

|
E4
|
Coefficient for strain rate effect in torsion
(Real)
|

|
K5
|
Stiffness for bending Y
(Real)
|
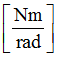
|
C5
|
Damping for bending Y
(Real)
|
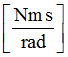
|
A5
|
Coefficient for strain rate effect in bending Y
Default = 1.0 (Real)
|

|
B5
|
Logarithmic coefficient for strain rate effect in bending Y
Default = 1.0 (Real)
|

|
D5
|
Scale coefficients for bending velocity
Default = 1.0 (Real)
|

|
Ascale5
|
Abscissa scale factor for 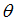 in bending Y (fct_ID15 and fct_ID35) in bending Y (fct_ID15 and fct_ID35)
(Real)
|

|
Hscale5
|
Coefficient for fct_ID45 in bending Y
Default = 1 (Real)
|
|
fct_ID15
|
Function identifier defining 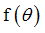 in bending Y in bending Y
If H5=4: Function identifier defining upper yield curve
(Integer)
= 0: linear spring
|
|
H5
|
Hardening flag
(Integer)
= 0: Nonlinear elastic spring
= 1: Nonlinear elasto-plastic spring
= 2: Nonlinear elasto-plastic spring with decoupled hardening in tension and compression
= 4: Nonlinear elastic plastic spring “kinematic” hardening
= 5: Nonlinear elasto-plastic spring with nonlinear unloading
= 6: Nonlinear elasto-plastic spring with isotropic hardening and nonlinear unloading
= 7: Nonlinear spring with elastic hysteresis
|
|
fct_ID25
|
Function identifier defining 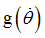 in bending Y in bending Y
(Integer)
|
|
fct_ID35
|
Function used only for unloading in bending Y
If H5=4: Function identifier defining lower yield curve
If H5=5: Function identifier defining residual displacement vs maximum displacement
(Integer)
|
|
fct_ID45
|
Function identifier defining 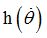 in bending Y in bending Y
(Integer)
|
|
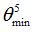
|
Negative failure limit
Default = -1030 (Real)
|

|
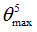
|
Positive failure limit
Default = 1030 (Real)
|

|
F5
|
Scale factor for 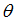 in bending Y in bending Y
(Real)
|

|
E5
|
Coefficient for strain rate effect in bending Y
(Real)
|

|
K6
|
Stiffness for bending Z
(Real)
|
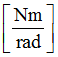
|
C6
|
Damping for bending Z
(Real)
|
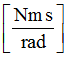
|
A6
|
Coefficient for strain rate effect in bending Z
Default = 1.0 (Real)
|

|
B6
|
Logarithmic coefficient for strain rate effect in bending Z
Default = 1.0 (Real)
|

|
D6
|
Scale coefficients for bending velocity
Default = 1.0 (Real)
|

|
Ascale6
|
Abscissa scale factor for 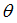 (fct_ID16 and fct_ID36) (fct_ID16 and fct_ID36)
(Real)
|

|
Hscale6
|
Coefficient for fct_ID46 in bending Z
Default = 1 (Real)
|
|
fct_ID16
|
Function identifier defining 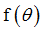 in bending Z in bending Z
If H6=4: Function identifier defining upper yield curve
(Integer)
= 0: linear spring
|
|
H6
|
Hardening flag
(Integer)
= 0: Nonlinear elastic spring
= 1: Nonlinear elasto-plastic spring
= 2: Nonlinear elasto-plastic spring with decoupled hardening in tension and compression
= 4: Nonlinear elastic plastic spring “kinematic” hardening
= 5: Nonlinear elasto-plastic spring with nonlinear unloading
= 6: Nonlinear elasto-plastic spring with isotropic hardening and nonlinear unloading
= 7: Nonlinear spring with elastic hysteresis
|
|
fct_ID26
|
Function identifier defining 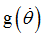 in bending Z in bending Z
(Integer)
|
|
fct_ID36
|
Function used only for unloading in bending Z
If H6=4: Function identifier defining lower yield curve
If H6=5: Function identifier defining residual displacement vs maximum displacement
(Integer)
|
|
fct_ID46
|
Function identifier defining 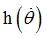 in bending Z in bending Z
(Integer)
|
|
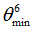
|
Negative failure limit
Default = -1030 (Real)
|

|
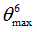
|
Positive failure limit
Default = 1030 (Real)
|

|
F6
|
Scale factor for 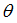 in bending Z in bending Z
(Real)
|

|
E6
|
Coefficient for strain rate effect in bending Z
(Real)
|

|
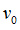
|
Reference translational velocity
Default = 1.0 (Real)
|
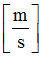
|
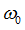
|
Reference rotational velocity in translation X
Default = 1.0 (Real)
|

|
c1
|
Relative velocity coefficient in translation X
Default = 0.0 (Real)
|
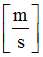
|
n1
|
Relative velocity exponent in translation X
Default = 0.0 (Real)
|
|
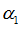
|
“Mult” factor in translation X
Default = 1.0 (Real)
|
|
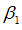
|
Exponent in translation X
Default = 2.0 (Real)
|
|
c2
|
Relative velocity coefficient in shear XY
Default = 0.0 (Real)
|
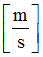
|
n2
|
Relative velocity exponent in shear XY
Default = 0.0 (Real)
|
|
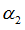
|
“Mult” factor in shear XY
Default = 1.0 (Real)
|
|
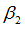
|
Exponent in shear XY
Default = 2.0 (Real)
|
|
c3
|
Relative velocity coefficient in shear XZ
Default = 0.0 (Real)
|
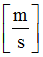
|
n3
|
Relative velocity exponent in shear XZ
Default = 0.0 (Real)
|
|
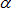 3 3
|
“Mult” factor in shear XZ
Default = 1.0 (Real)
|
|
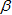 3 3
|
Exponent in shear XZ
Default = 2.0 (Real)
|
|
c4
|
Relative velocity coefficient in torsion
Default = 0.0 (Real)
|

|
n4
|
Relative velocity exponent in torsion
Default = 0.0 (Real)
|
|
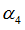
|
“Mult” factor in torsion
Default = 1.0 (Real)
|
|
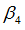
|
Exponent in torsion
Default = 2.0 (Real)
|
|
c5
|
Relative velocity coefficient in bending Y
Default = 0.0 (Real)
|

|
n5
|
Relative velocity exponent in bending Y
Default = 0.0 (Real)
|
|
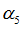
|
“Mult” factor in bending Y
Default = 1.0 (Real)
|
|
|
Exponent in bending Y
Default = 2.0 (Real)
|
|
c6
|
Relative velocity coefficient in bending Z
Default = 0.0 (Real)
|
|
n6
|
Relative velocity exponent in bending Z
Default = 0.0 (Real)
|
|
|
“Mult” factor in bending Z
Default = 1.0 (Real)
|
|
|
Exponent in bending Z
Default = 2.0 (Real)
|
|