HMath-5001: Post-processing Results from FEA

HyperMath contains a set of commands to read data from a variety of file types. Supported file types include simple column ASCII data to the binary result formats supported in other HyperWorks programs like HyperView and HyperGraph.

This tutorial demonstrates the application of custom post-processing to a finite element analysis. Specifically, reading in the forces from 1D beam elements and creating a scatter plot of the normal and shear forces in the elements.

The target file in for this problem is the BeamElementresults.h3d, located in [install_directory]\tutorials\hmath.

Step 1: Get the target filename and read the table of contents.

1.	Start HyperMath.

2.	In a new script, type the commands listed below. The first command opens a standard Tcl/Tk dialogue that you can use to select a target file and saves the complete path to the file in the Tcl variable myFile. The second command sets the HyperMath variable fileName to the Tcl variable myFile.

EvalTclScript("set myFile [tk_getOpenFile -title \"Select Data File\"]")

fileName = GetTclVar('myFile')

3.	Next, extract the file’s table of contents to understand the file structure. This is crucial for the proper definition of the extracted results. Type the command:

toc=ReadFileToc(fileName)

4.	Run the script. In the Variable Browser, a table named toc contains the table of contents for the result file. Expanding the table hierarchy exposes the information contained in the file such as subcases, types, requests, and components.

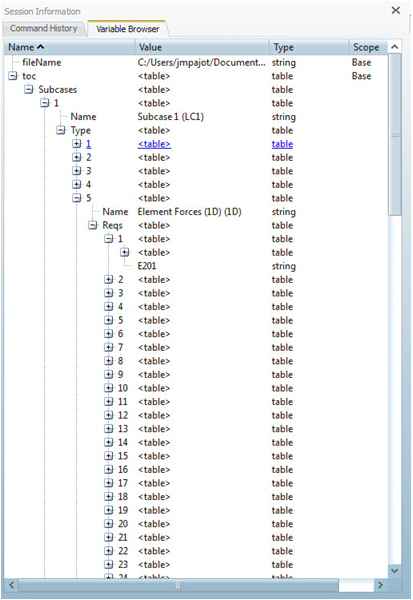
hmath_5001_img1

Step 2: Define the required extraction information.

1.	Based on the table of contents, the correct names of the result type to collect 1D forces is set. This model contains a single subcase, so the subcase ID is set to 1. Similarly, we can set the component names for the normal and shear forces as well.

subcaseNum=1

typeName="Element Forces (1D) (1D)"

normalName="CBAR/CBEAM Axial Force A"

shear1Name="CBAR/CBEAM Shear Plane-1 A"

shear2Name="CBAR/CBEAM Shear Plane-2 A"

2.	There is more than one available element in the list of result requests. In this case, the goal is to work with all of the available results. The following lines query the subcase for a list of the available elements for the given type.

s=GetSubcase(fileName,subcaseNum)

typeIndex= s::GetTypeIndex(typeName)

numReq=s::GetNumReqs(typeIndex)

reqList=s::GetReqList(typeIndex)

Step 3: Loop over the elements and extract the data.

1.	The HyperMath command ReadVector reads the data for each record one line at a time. In this example, the data is stored into vectors, which are initialized to empty.

n=[]

s1=[]

s2=[]

for ix = 1,numReq do

n(ix)=ReadVector(fileName,1,typeName,reqList[ix],normalName)

s1(ix)=ReadVector(fileName,1,typeName,reqList[ix],shear1Name)

s2(ix)=ReadVector(fileName,1,typeName,reqList[ix],shear2Name)

end

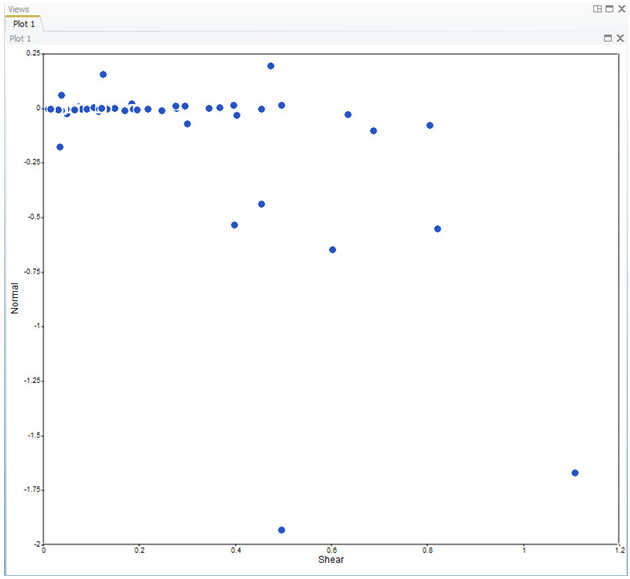
Step 4: Compute the magnitude of the shear forces and plot the data.

1.	With the normal, shear1, and shear2 forces stored for each element, compute the combined shear stress for each element with a term-by-term multiplication of the vectors

sC=Sqrt(s1.^2+s2.^2)

2.	Plot the data in a scatter plot, turn the legend off, and label the axes.

PlotScatter(sC,n)

LegendOff()

SetXLabel("Shear")

SetYLabel("Normal")

hmath_5001_img2

HMath-5001: Post-processing Results from FEA

HMath-5001: Post-processing Results from FEA

HMath-5001: Post-processing Results from FEA

See Also: