Term

Description

Study

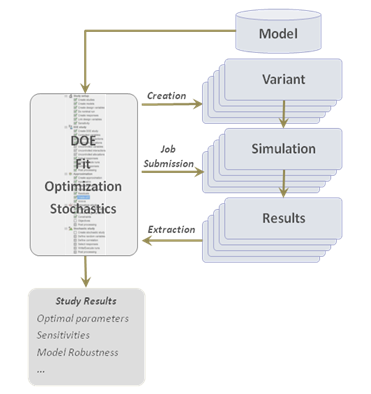
A HyperStudy session or .xml file that contains the study Setup and study approaches. Among other objectives, you can setup a study to understand the relationship between the input and output of a system in order to find the best design for a given design criteria.

Model

A model is part of a study. It is the model of the system that is subjected to a study. In each study, you can add one or more models.

Types of models include:

Input Variable

System parameters that you can change to improve the system performance.

Examples of input variables are beam dimensions, material properties, diameter, and number of bolts.

Specifications

A specification is a set of requirements the study Setup or approach needs in order to run.

Nominal Run

Runs one simulation where the input variable's values are set to the initial values.

System Bound Check

Checks the study setup and the design space using three runs. The first run sets all of the input variables to their nominal values, the second run sets all of the values to their lower bounds, and the third run sets all of the values to their upper bounds.

Sweep

Evaluates design alternatives for a study where the input variable values increase in equal increments.

Output Response

A measurement of system performance.  For example: weight, volume, displacement, stress, strain, reaction forces, and frequency.

Approach (Study Approach)

A study approach is a specific set of steps taken to study the mathematical model of a design. In HyperStudy, there are four different approaches:

Each approach serves a different purpose in the design study. The required steps for each approach may be unique. For example, you can use the DOE approach if you need to learn the main factors affecting your design, but you need to use the optimization approach if you want to find the design that achieves the design objectives while satisfying design requirements.

Design of Experiments (DOE) Approach

A series of tests in which purposeful changes are made to the input variables to investigate their effect upon the output responses and to get an understanding of the global behavior of a design problem.

Levels

The number of levels per variable to be considered, depends on the level of non linearity in the problem. Two levels are sufficient for a linear model, whereas three levels are required for a quadratic model.

Effects

If the effects line is horizontal, it implies that the input variable has no effect on the output response of interest. As the line becomes more vertical, the effect on the output response of interest is greater. A positive slope indicates that changing the parameter value will result in a direct change to the output response, whereas a negative slope indicates an inverse association.

Fit Approach (Approximation)

A Fit approach is used to construct a mathematical function that best fits to a dataset imported from a DOE or a stochastic approach. This mathematical function can then be used instead of the exact solvers in other approaches to save computational resources.

Input Matrix

A collection of designs that are used to build a response surface.

Validation Matrix

A collection of designs that are used to verify the quality of a response surface.

Residuals

The difference between the response value from the solver and the response value from the response surface is the error, or the residual. The residual plot can be used to determine which runs are generating more error in the model.

Diagnostics

Diagnostics help to assess the accuracy of the response surface.

Optimization Approach

An Optimization approach is a mathematical procedure used to determine the best possible design for a set of given constraints, by changing the input variables in a defined manner.

Objective

Any output response functions of the system to be optimized. The output response is a function of the input variables.  Examples: Mass, Stress, Displacement, Frequency, etc.

Constraint

Bounds on output response functions of the system that need to be satisfied for the design to be acceptable.

Optimum Design

Set of input variables along with the minimized (maximized) objective function that satisfies all of the constraints.

Stochastic Approach

Stochastic approaches are used in order to study the effects of design variations in the design performance. These variations may occur due to manufacturing, operating environment, etc. The result of a stochastic analysis is an output response value with a distribution.

Reliability

Analysis to find the probability with which a design will fail or succeed.

Study Question or Scenario

Best HyperStudy Options

I have a RADIOSS model that I want to do  a size/shape optimization study with. I will run the simulations in my PC.

Once you are finished creating your shape variables in HyperMorph, start HyperStudy from HyperMesh's Applications menu. Your model type is “HyperMesh”.

I have a MotionSolve model. I will run the simulations in my PC.

Start HyperStudy from MotionView's Applications menu.  Your model type is “MotionView”.

I am using a commercial solver that is not in  HyperWorks, but it integrates with HyperWorks (Abaqus, LS-DYNA, DesignLife, etc.). I would like to set up a size optimization study and will run the simulations in a cluster.

Start HyperStudy in standalone mode. Your model type is “Parameterized File”. You can create the parameterized file by using the Editor option under the Tools menu. Register the solver by using the Register Solver Script option in the Edit menu.

I did my analysis in a spreadsheet. Some of the cells are input variables and some are output responses.

Start HyperStudy in standalone mode. Your model type is “Spreadsheet”.

I calculated my output reponses using analytical equations.

Start HyperStudy in standalone mode. Your model type is “Internal Math”.

Study Approach Question or Scenario

Best HyperStudy Options

Which input variables have a significant effect on my output responses?

Use a parameter screening DOE, such as Fractional Factorial. Once the parameter screening DOE is complete, look at the Effects and Interactions plots.

How can I do quick trade-off studies?

Use a space-filling DOE to create fitting functions to your output responses.

What are the best input variable values to minimize my objective, while meeting my design requirements?

Use a single objective optimization, such as ARSM, SQP, MFD  or GA.

What is the reliability of my design?

Use a Stochastic approach and add your reliability assessment.